昨天在doyoudo上面看到了有Low poly的视频教程,觉得现在Lowploy风格的图画还是非常棒的,于是也想自己动手试一试。一番尝试之后,发现最麻烦的还是网格设置。如果能够在图片上批量生成网格,那么制作Lowpoly的过程会简单很多。仔细想一下会发现,这个网格的生成似乎和有限元网格的生成有点像,于是就想分析一下Mathematica是怎么生成这个网格的。如果只是单独的随便生成三角形的网格那么就太低端了,所以这篇文章不仅生成比较好看的网格,还能进行编号。
1.基础知识
有限元网格是用来对复杂模型进行计算的最基础的一步。一般来说,一个比较复杂的受力模型想要获得其解析解是不可能的,即便是弹性力学也只是局限于规则的图形。通过网格划分,可以将一个复杂的模型2D模型划分成简单的三角形或者四边形。3D模型一般是划分为四面体或者六面体。然后运用形函数描述这个基本图形。最后将这些简单的基本图形组成矩阵进行计算,即可计算得到每一个小的基本图形的数值解。这样就近似的完成了整个模型的计算。
所以在模型计算的过程中,网格划分是至关重要的一步,好的网格可以提高模型的计算精度和计算速度,而比较糟糕的网格则会引起收敛性的问题。本文将会用一个简单的圆管作为分析来划分出一个比较好看的有限元网格。当然在自己分析的过程中遇到了一些难题是在mathematica的论坛上得到解决的。
首先我们来观察一个基本的有限元模型网格:

MMA划分有限元网格
这个是最简单的一种划分形式,网格比较乱,且没有什么规则。我们的目标是划分一个比较好的网格。
2.数据生成
要划分网格首先需要有基本的数据点,因此我们需要先在MMA中生成网格数据点,这里采用同心圆的方式进行生成:
|
1 2 3 4 5 6 |
Clear["Global`*"] Needs["NDSolve`FEM`"] nCircle = 5; nSect = 16; ring = Table[r {Cos[\[Phi]], Sin[\[Phi]]}, {r, 1, nCircle}, {\[Phi], 0, 2 \[Pi] - 2 \[Pi]/nSect, 2 \[Pi]/nSect}] // N; |
其中nCircle表示圆环个数,nSect表示环向分割数。这里注意开头的第二行,需要调用MMA的有限元模块,这样网格的计算和布置将会很方便。计算完成之后就可以得到下面的散点:
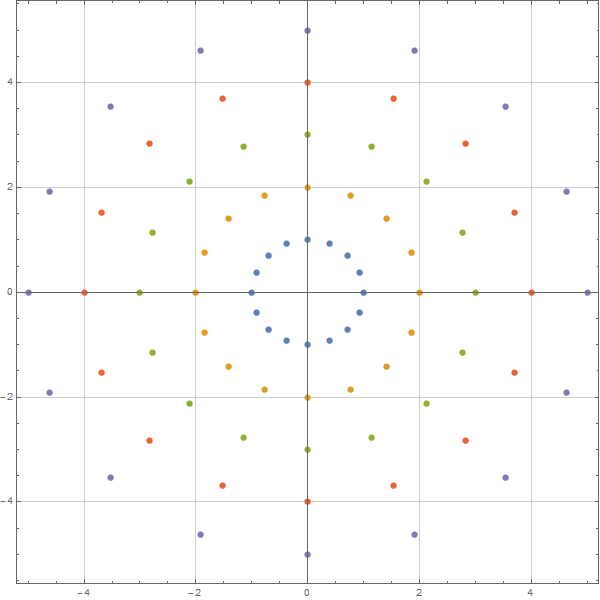
MMA划分有限元网格
我们将以上面的散点作为有限元网格的节点,生成有限元网格。
3.节点编号
在有限元网格中,需要对网格进行逆时针编号,这样可以保证形函数计算过程得到的是正值。先分析下面这样一张图:
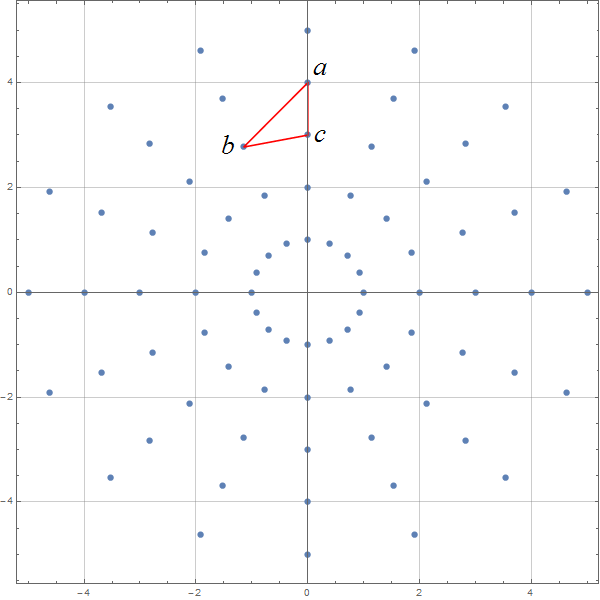
MMA划分有限元网格
按照逆时针的编号规则,我们先计算\(a\)的坐标,然后是\(b\)的坐标,最后是\(c\)的坐标。
在进行具体做操作之前,我们先分析一个难点,就是这个\(b\)点坐标问题,因为我们采用列表循环进行编号分配,当循环一圈之后\(b\)点会与\(c\)点重合。这时候的编号应该应该是\(c\)点点对应的编号,因为在有限元中每一个节点的编号是位移的。
举个简单的例子,比如按照\(x+1\)、\(y+2\)、\(y+1\)进行\(a\)点、\(b\)点、\(c\)点编号,那么循环一圈之后,最后一个三角形中的编号应该是\(x+16\)、\(y+1\)、\(y+16\),而不是\(x+16\)、\(y+17\)、\(y+16\)。那么这个就需要用到一个技巧,就是使用Mod[ ]函数,这个函数是取余数,但是如果是Mod[x,y]那么在\(x=y\)的时候,结果为0,这不是我们想要的,所以可以使用这个函数的第三个参数\(d\),这个参数的使用可以产生\(1 \Rightarrow y\)而不是\(0 \Rightarrow y-1\)的数值。
|
1 2 3 |
inc1 = Table[{nSect (i + 1) + j, nSect i + Mod[1 + j, nSect, 1], nSect i + j}, {i, 0, nCircle - 2}, {j, 1, nSect}]; inc2 = Table[{nSect (i + 1) + j, nSect (i + 1) + Mod[1 + j, nSect, 1],nSect i + Mod[1 + j, nSect, 1]}, {i, 0, nCircle - 2}, {j, 1, nSect}]; inc = {inc1, inc2}; |
这样可以生成其中节点的编号规则,这个编号规则按照点的顺序开始,不能矛盾,否则MMA将会返回编号失败的信息。
但是在具体网格划分之前先进行压平处理,因为上面生成的inc是一个四维的矩阵:
|
1 |
triangles = Flatten[inc, 2]; |
这样可以压缩成由编号组成的二维矩阵。
4.网格生成
如果已经将点和编号处理好的话,那么只需要进行一个简单的命令就可以生成网格:
|
1 2 |
mesh = ToElementMesh["Coordinates" -> points, "MeshElements" -> {TriangleElement[triangles]}]; mesh["Wireframe"] |
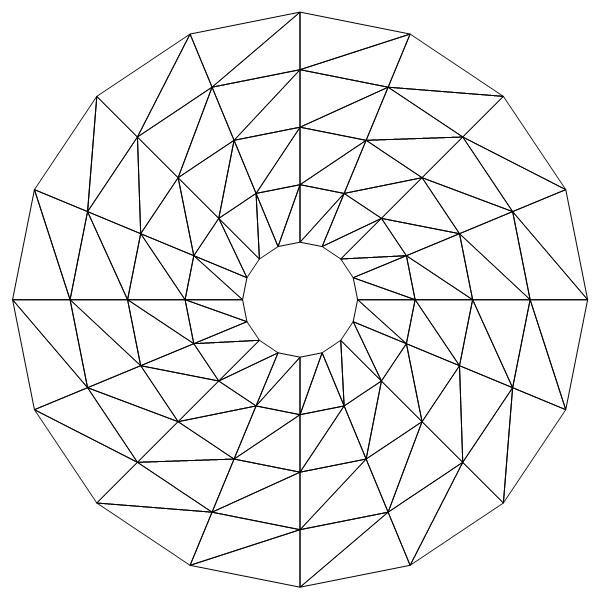
MMA划分有限元网格
可以通过下面的方式显示节点的编号:
|
1 |
Show[mesh["Wireframe"],mesh["Wireframe"["MeshElement" -> "PointElements", "MeshElementStyle" -> Directive[Red, PointSize[0.01]],"MeshElementIDStyle" -> Blue]]] |
得到下面的图片:
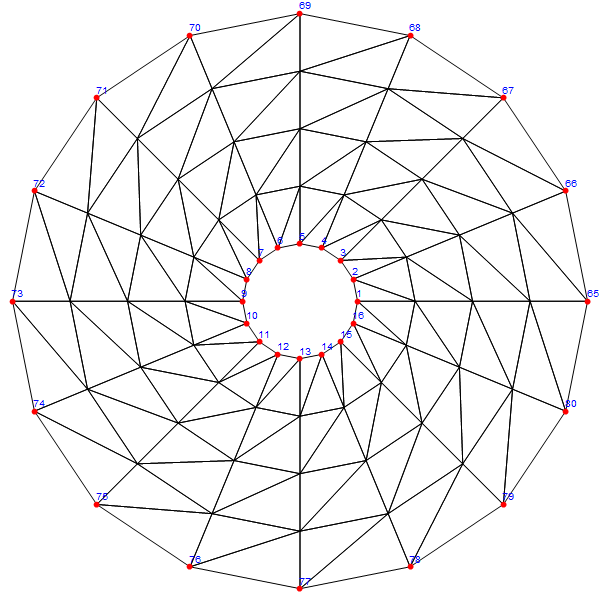
MMA划分有限元网格
5.End小结
这个其实还是比较好做的,最关键的就是自己图片编号的处理,不过话说我把参考的那个文章给弄丢了,也不知道放到哪里去了,就不写参考了。
给出一个文中代码的下载链接:Qn99E5.zip




