上次根据地震波加速度计算了地震波的速度和位移时程,之后便考虑是否可以直接算出这个地震波的反应谱。考虑到Mathematica自带了微分方程求解器,这样求解二阶微分方程可以不用自己手动编写程序,会方便很多。于是本文将借用MMA自带的NDSolveValue计算地震波的反应谱。
1.基础知识
所谓的反应谱,根据结构动力学书上的介绍,是线性单自由度体系对于地面运动的某个特定分量的峰值反应的所有值。简单来说,将单自由度体系的某个固定参数,比如振动周期Tn可以作为自变量,然后结构体系的峰值位移umax作为因变量。
这样的一类图形是针对一个固定的阻尼比的,那么针对不同阻尼比是可以获得不同的反应谱。在实际使用中,一般是将多个不同阻尼值得反应谱联合起来使用,这样基本可以覆盖各种实际结构的阻尼。对于计算的反应谱,自变量选择频率还是周期是随意的。一般比较多的是以周期为自变量的。规范的谱也是以周期为自变量的。
反应谱的种类有很多,一般结构动力学上最常用的就是位移、速度和加速度谱:
\[\begin{array}{l}
{u_0}({T_n},\varsigma ) = \mathop {\max }\limits_t \left| {u(t,{T_n},\varsigma )} \right|\\
{{\dot u}_0}({T_n},\varsigma ) = \mathop {\max }\limits_t \left| {\dot u(t,{T_n},\varsigma )} \right|\\
{{\ddot u}_0}({T_n},\varsigma ) = \mathop {\max }\limits_t \left| {\ddot u(t,{T_n},\varsigma )} \right|
\end{array}\]
本次我们将针对周期Tn为自变量,计算一个地震波的位移谱。
2.计算过程
首先还是先获得一条地震波,地震波这里还是采用Elcentro波,这个波可以去vibrationdata下载。下载下来的地震波是已经进行过矫正的,因此不再需要进行额外的处理。将这个地震波导入MMA中:
|
1 2 3 4 5 6 |
Clear["Global`*"] data = Import[NotebookDirectory[] <> "elcentro.dat"]; acc = Interpolation[data] tmin = (Min /@ Transpose[data])[[1]]; tmax = (Max /@ Transpose[data])[[1]]; Plot[acc[x], {x, tmin, tmax}, PlotRange -> All, Frame -> True, GridLines -> Automatic, ImageSize -> 600] |
这里的处理和之前的地震波的速度和位移时程是一样的,可以直接绘制出地震波的时程曲线:
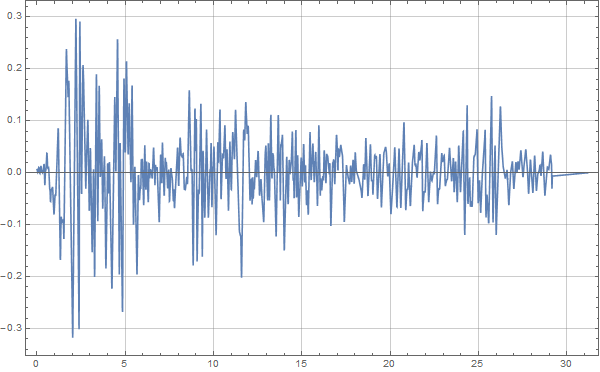
MMA地震波反应谱计算
然后设置这个激振的单自由度体系的一些基本参数:
|
1 2 3 4 5 |
dampRatio = 0.02; sampleTime = 10; samplePoint = 10; eigenPeriod = Table[i, {i, sampleTime/samplePoint, sampleTime, sampleTime/samplePoint}]; dispSet = Table[0, {samplePoint}]; |
这里设置了阻尼比为0.02,计算周期是10s,设置10个采样点进行计算。这里要注意的是有必要将存储峰值位移的变量进行初始化一下,不然后期会产生错误。
导入地震波绘图时我们已经获得了加速度的插值函数acc。因此acc[t]就表示在t时间的地面加速度值。根据动力学基本方程:
\[\ddot u + 2\varsigma {\omega _n}\dot u + \omega _n^2u = – {\ddot u_g}(t)\]
上式中右侧的地震加速度就是我们获得的acc[t]这个函数,可以直接带进去,MMA能够自动计算。结合For循环,计算循环十次下的峰值:
|
1 2 3 4 5 6 |
For[i = 1, i <= samplePoint, i++, disp = NDSolveValue[{u''[t] + 2*dampRatio*(2*Pi/eigenPeriod[[i]])*u'[t] + (2*Pi/eigenPeriod[[i]])^2*u[t] == -9.8*acc[t], u'[0] == 0, u[0] == 0}, u, {t, tmin, tmax}] ; dispSet[[i]] = Max[Abs[Table[disp[x], {x, tmin, tmax, (tmax - tmin)/Length[data]}]]]; ] points = Transpose[{eigenPeriod, dispSet}]; ListLinePlot[points, PlotRange -> All, Frame -> True, GridLines -> Automatic, ImageSize -> 600] |
这样就可以得到一张简单的位移谱:
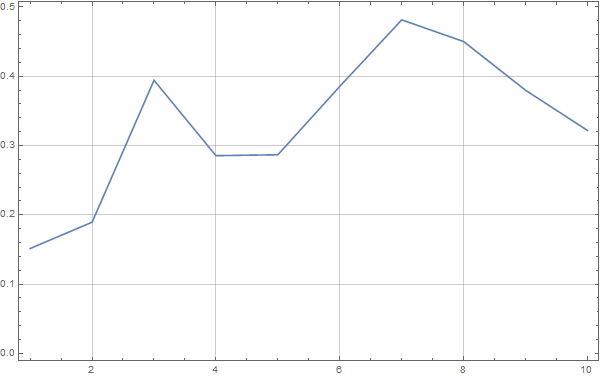
MMA地震波反应谱计算
当然这张谱是非常粗糙的,这个可以通过调节采样值,从而获得不同的精细度。
3.SeismoSignal对比
上面只是单纯的计算,为了获得准确地反应谱,需要将结算的结果和通用的软件对比一下。上次采用的DPLOT已经被我卸载了,因为不兼容。关闭DPLOT退出的时候,它的进程不退出,导致卡系统,另外DPLOT比较丑。这次我采用了SeismoSignal来对比。
将数据文件导入SeismoSignal后切换到Elastic/Inelastic Response Spectra界面,直接获取地震数据的反应谱,我们将获得的位移谱保存下来并导入MMA进行对比:
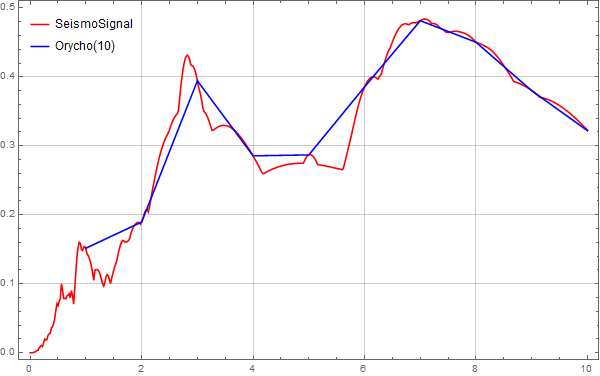
MMA地震波反应谱计算
可以发现二者大致的趋势是一致的,现在将程序中的采样点分别修改为50、200、500和1000进行计算和对比。
下图是采样点为50的对比图:
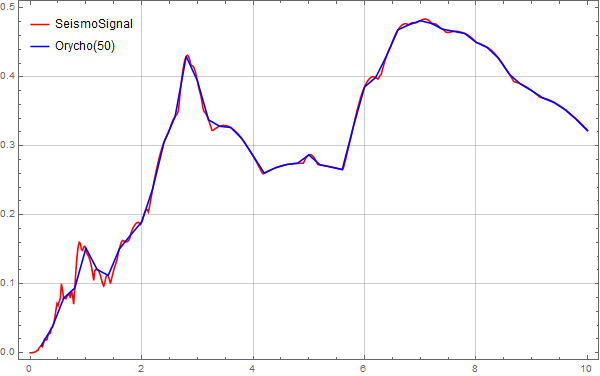
MMA地震波反应谱计算
下图是采样点为200的对比图:
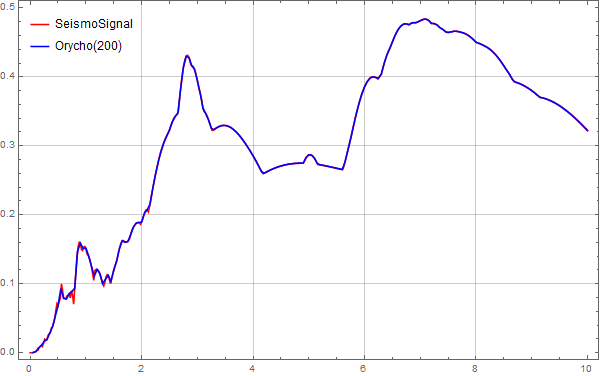
MMA地震波反应谱计算
下图是采样点为500的对比图:
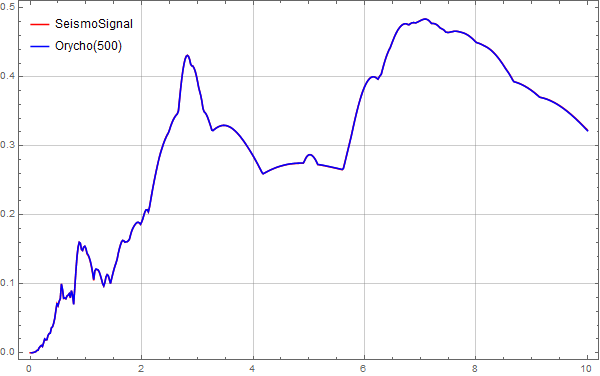
MMA地震波反应谱计算
下图是采样点为1000的对比图:
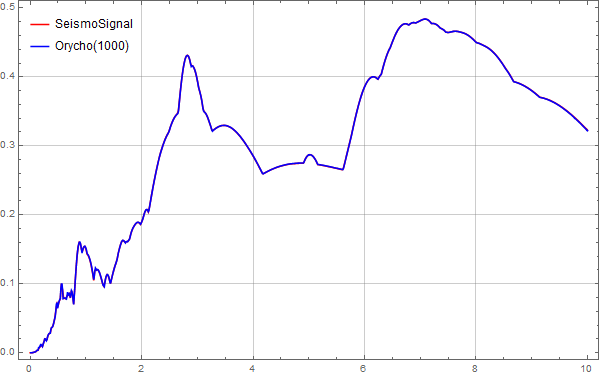
MMA地震波反应谱计算
从上面的图片看出,在采样点达到500时,由MMA计算的位移谱已经和SeismoSignal的数据匹配的非常好了。
4.缺陷及建议
虽然MMA的计算结果与常用软件的计算结果吻合的非常好,但是这个方法的计算速度太慢了。如果试过的话,可以发现在采样点选择1000次的时候,需要长时间的等待,这与SeismoSignal的差距很大,一般来说,反应谱在加速度导入的时候可以快速的计算出来,因此上面的方法有待改进。
最常用的可以用NewMark法进行这样的计算,在动力学的书中也有很多的介绍。之所以本文采用上面的方法,是因为这样的方式是最简单,也是充分发挥一下MMA的功能。但所带来的劣势就是要消耗大量的时间。
5.End小结
这个算法就先弄到这里,不再额外的编写微分方程求解算法加速了,如果需要更快速地计算,直接用动力学的书上的方法就可以。
下次有时间再写一个常规的算法求解一下。
给出一个文中代码的下载链接:Cs20v0.zip




