之前做时程分析的时候用过SeismoSignal是SeismoSoft公司出品的一款地震波处理软件,可以对地震波进行滤波、基线调整、位移谱计算等等。当时觉得这个软件做的非常不错,用起来也很顺手,就想自己是不是也可以这样弄一个玩玩。于是我们要分析分析目标。
- 各种滤波:高通滤波、低通滤波、带通滤波;
- 速度和位移时程计算;
- 基线矫正;
- 傅里叶变换;
- 计算速度和位移谱
其实最简单的就是能够将地震波进行积分获得速度和位移曲线,我当时就想单独实现这个目的。本来以为这个很简单的,但是知道自己亲自试试,才发现没有那么容易。下面就记录一下整个分析的过程。
1.计算原理
原理很简单,但是却不是很好实现。平时获得的地震数据都是加速度时程曲线,按照基本物理学知识,在假设初速度为零的情况下,只要对这个加速度曲线进行积分就可以得到速度。然后对速度积分就可以得到位移。
按照这个原理要获得速度和位移在某一个点的值是很好办,但是要计算出速度和位移的时间曲线就比较麻烦了。除了我们后面要处理的基线矫正的问题之外,我们还要进行大量的积分计算。详细分析一下:
\[v(t) = \int_0^t {a(t)dt} \]
其实不难发现,如果说加速度有2000个数据点,那么为了获得速度曲线,就必须要算出几千个数据点,那么就要不断地针对上面的积分变换上限计算,计算机几千次的积分,即便是MMA或者MATLAB也是很有压力的。所以当想要用绘图命令绘制一个20s的速度曲线的时候,那绝对是没有希望的。
|
1 |
Plot[NIntegrate[acc[t], {t, 0, x}], {x, 0, 20}] |
所以我们需要变换一下思路:将积分求解器更换成微分求解器。
在数值计算中,常微分方程的数值解求解算法的计算速度是客观的,因此我们用下面的表达式进行求解:
\[\frac{{dv(t)}}{{dt}} = a(t)\]
然后使用常微分方程求解器求解其中的速度分量。
2.速度时程计算
根据上面的分析,就可以直接开始进行计算了,首先将常用的地震波Elcentro波的数据下载下来,并采用Import[ ]函数读取进来:
|
1 2 3 4 5 6 |
Clear["Global`*"] data = Import[NotebookDirectory[] <> "elcentro.dat"]; acc = Interpolation[data]; tmin = (Min /@ Transpose[data])[[1]]; tmax = (Max /@ Transpose[data])[[1]]; Plot[acc[x], {x, tmin, tmax}, PlotRange -> All, Frame -> True, GridLines -> Automatic, ImageSize -> 600] |
要注意一下,开始一定要先Clear[ ] 清理一下内存,不然后面会发生很多怪异的问题!然后读取进来之后,直接获得地震波的起止时间tmin和tmax,并用Plot[ ] 函数绘制一下加速度时程曲线:
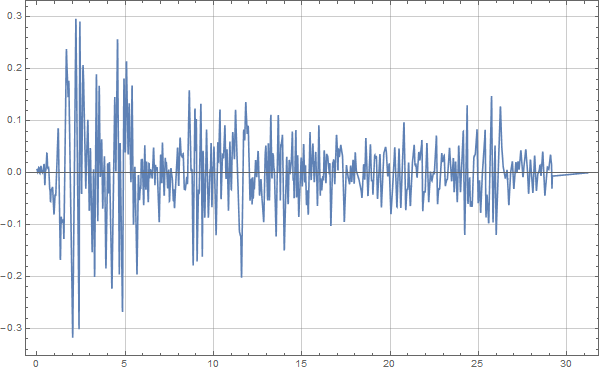
MMA地震波时程积分
获得这张数据图之后就可使用内置的常微分方程求解器计算这个速度:
|
1 |
velo = NDSolveValue[{velo'[x] == acc[x], velo[0] == 0}, velo, {x, tmin, tmax}]; |
这里的velo即是常微分方程求解器计算的结果,我们可以使用Plot[ ]绘制一下这个曲线:
|
1 |
Plot[velo[x], {x, tmin, tmax}, PlotRange -> All, Frame -> True, GridLines -> Automatic, ImageSize -> 600] |
曲线如下图所示:
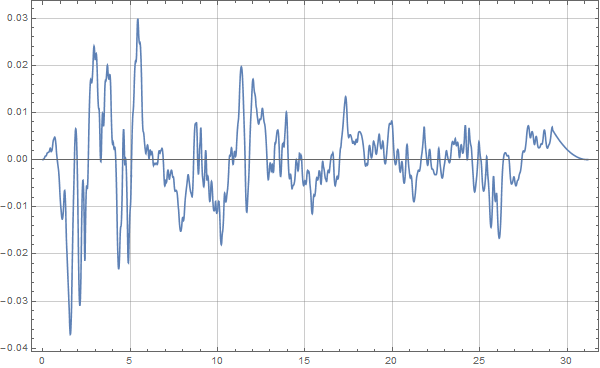
MMA地震波时程积分
这张图看着还是很不错的。起码已经有我们需要的结果了。
3.基线修正
在获得速度曲线之后,要进行一个重要的步骤就是基线修正。因为我们所得到的加速度数据其实是地震过程中的一部分,而由于加速度传感器灵敏度的问题,我们不能获得0时刻以前的数据,但由于轻微地震,确实是有数据的。另外就是在加速度传感器记录加速度的过程中会产生误差,也会产生零飘现象。现在我们假设这段地震波发生前后地面是静止的,也就是速度为零。因此我们要稍微修正一下这个地震波。
由于我这个是下载的标准地震波,是修正过的,因此上面的速度曲线已经是近乎完美了。
根据基本的拟合方程,直接进行一个回归计算,拟合一个函数出来:
|
1 |
velofit = Fit[{{tmin, velo[tmin]}, {tmax, velo[tmax]}}, {1, x, x^2}, x]; |
可以得到这么一个回归函数:
$$y = – 2.396 \times {10^{ – 21}} + 3.202 \times {10^{ – 7}}x + 1.027 \times {10^{ – 8}}{x^2}$$
这个函数是非常小,基本没有什么修正,但是为了完成整个分析,还是要按照下面的方法再次计算这个速度曲线:
|
1 2 |
velonew = velo[x] - velofit; Plot[velonew, {x, tmin, tmax}, PlotRange -> All, Frame -> True, GridLines -> Automatic, ImageSize -> 600] |
这样我们可以得到下面的曲线:
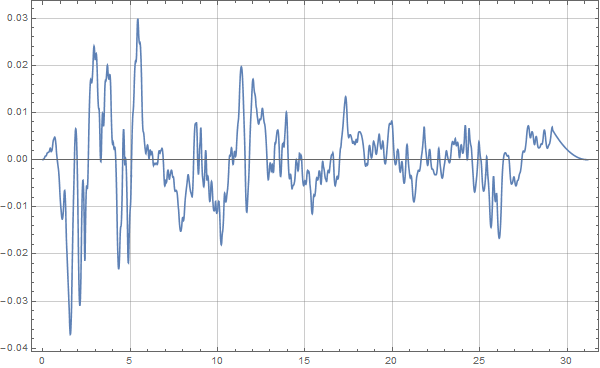
MMA地震波时程积分
感觉这个曲线好像并没有什么差别的样子。
4.位移时程计算
得到速度时程之后,我们采用同样的方式进行位移时程的计算:
|
1 2 |
disp = NDSolveValue[{disp'[x] == velonew, disp[0] == 0}, disp, {x, tmin, tmax}]; Plot[disp[x], {x, tmin, tmax}, PlotRange -> All, Frame -> True, GridLines -> Automatic, ImageSize -> 600] |
这样我们就顺利的得到了Elcentro地震波的位移时程曲线了:
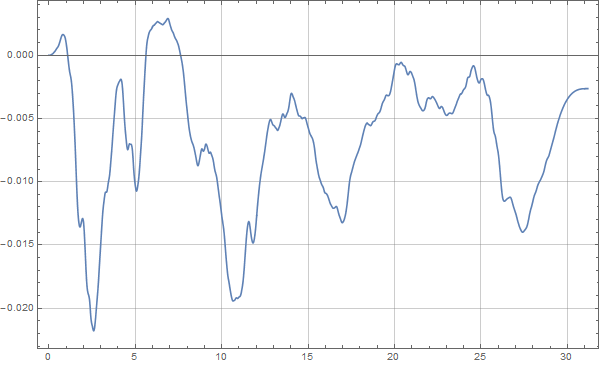
MMA地震波时程积分
但是我们发现这个位移时程也是有点“问题”的,地震结束之后地面存在永久位移。对于这个问题,其实并不是没有可能,但是有时候我们也对位移进行一定的修正,用于模型的分析。这次明显一点,我们设置一个三次的回归函数,并在原图上绘制出来:
|
1 2 3 4 |
trend = disp; fit = Fit[{{tmin, trend[tmin]}, {tmax, trend[tmax]}}, {1, x, x^2, x^3}, x]; removetrend = disp[x] - fit; Plot[{disp[x], fit}, {x, tmin, tmax}, PlotRange -> All, Frame -> True,GridLines -> Automatic, ImageSize -> 600] |
可以得到下面的曲线:
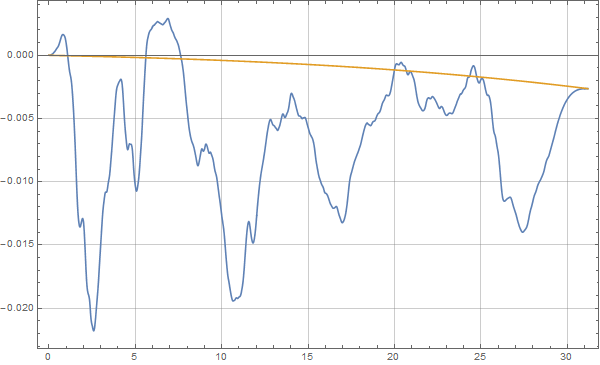
MMA地震波时程积分
然后我们去除这个基线偏移值就可以得到没有零飘的位移时程了:
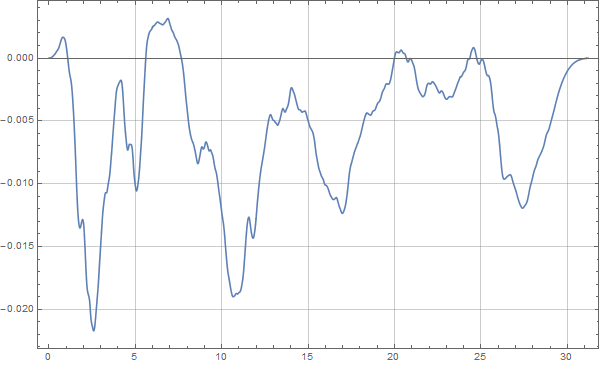
MMA地震波时程积分
5.DPLOT验证
为了检验我们的分析计算结果,我采用了DPLOT这个软件验证一下,这个软件有点类似于SeismoSignal软件,但是没有后者那么高级,算是一个简单是数据处理软件。不过貌似官方售价并不便宜。
将曲线导入DPLOT中,然后点击积分按钮两次,可以得到位移曲线,然后再Edit->Remove Trend可以去除零飘现象。然后将数据导出,我们对比一下:
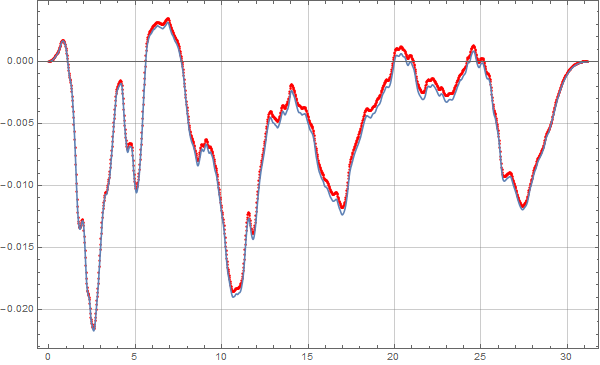
MMA地震波时程积分
红色的线是DPLOT的结果,蓝色的线是我们计算的结果。我们发现好像有点误差,其实这并不是计算有问题,是我们在修正的时候采用了三次拟合函数进行修正的,下面我直接用一次函数修正这个零飘现象并对比:
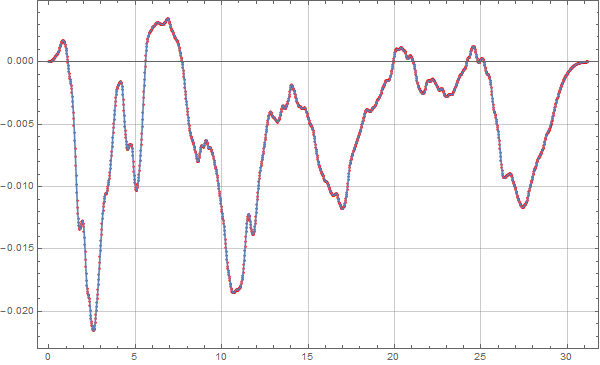
MMA地震波时程积分
大家可以发现,这两者的计算结果基本一致。这里要注意的是由于地震波是修正过的,所以速度是否修正无关紧要。那么从这里就可以发现,DPLOT的Remove Trend是一个一次函数的修正。
6.End小结
这个也是基本花了一天的时间来完成了,做做GRE阅读就过来弄弄这个地震波积分,然后在它积分的过程中,再做两篇阅读。不过后来发现这个微分求解替代积分的方案之后一下节省的好多时间。
给出一个文中代码的下载链接:FF66n8.zip
最后感谢一下Reference中的作者们~
话说这个Ghost博客客户端在文章内容比较多的时候,真心是有点卡啊。卡的为都怀疑是不是输入法坏掉了,但是切换回到网页上面又没有问题。。。




