本文采用ANSYS对在实际使用中的扳手进行可靠性分析，扳手在实际使用中，正六边形的六个角点固定不动，在手柄处施加荷载，尺寸如下所示：

根据强度理论分析，假设在施力过程中，应力不允许超过屈服强度，超过了屈服强度则认为扳手失效，则扳手的失效准则为：

\[{\sigma _{\max }} \ge \sigma _{s } \]

则可以设置极限状态函数为：

\[G(x) = {\sigma _s} – {\sigma _{\max }}\]

如果出现G(x)<0，则可以认为扳手失效，其中x为所有不确定因素组成的向量，本文求解G(x)>0的概率。

首先建立模型，在进行概率分析之前需要做的是，采用APDL建立一个干净的命令流模型或者采用GUI操作并记录LOG文件之后整理成干净的且可以正常执行的命令流程序，这是必要的，因为在进行概率分析时需要反复的建模，因此在进入PDS模块时需要指定所分析问题的APDL文件。

本文为方便起见，全部采用命令流建模，以达到减小不必要错误的目的。建模初期先确定基本尺寸，之后将所需要改变的不确定因素(例如：宽度、长度、荷载等)的基本尺寸全部赋予相应的变量，在建模中使用变量名进行建模，保证模型顺利建立，并完成一次分析。

扳手模型采用壳单元SHELL63建立，建立过程较为简单，直接生成模型：

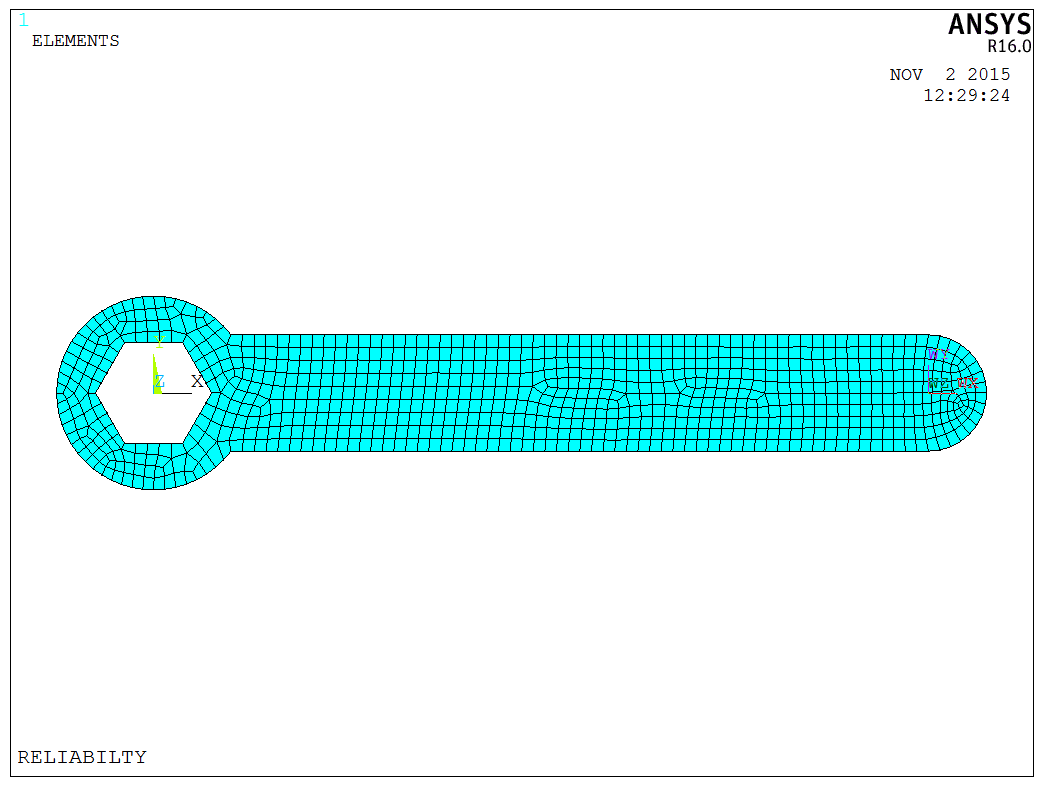
模型建立

由于我们的目标是获取构件的最大内力并与标准的屈服应力相比较，因此在APDL中可以先使用NSORT命令，对所有节点按照应力进行排序，之后用*GET获取最大应力点的应力值。

定义G(x)函数对应的变量名并赋值，这样可以在ANSYS的Scalar Parameters中查看，这里定义的变量名称为DETSS：

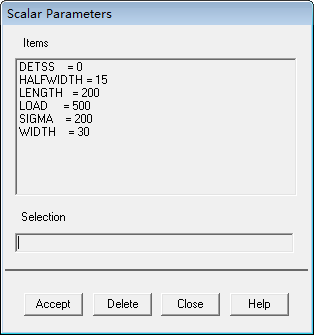
失效函数

在顺利的完成上述分析时，采用LGWRITE命令，将我们所做的一次完整的分析过程以命令流的方式写入文件。

进入PDS分析模块，可以在ANSYS界面中点击Prob Design，也可以在命令流中/PDS进入，之后指定分析所需的文件，即刚才写入的文件：

分析文件

之后按照概率分析列表的顺序，定义输入的变量，这里输入变量包括长度，宽度和荷载等，可以采用PDVAR进行定义，在进行定义的时候需要指定其概率分布类型，误差一般以高斯分布，其他的可以参考相关的概率书籍。(此处定义的变量为分析文件初始时设置的不确定因素的变量，名称要一致。)

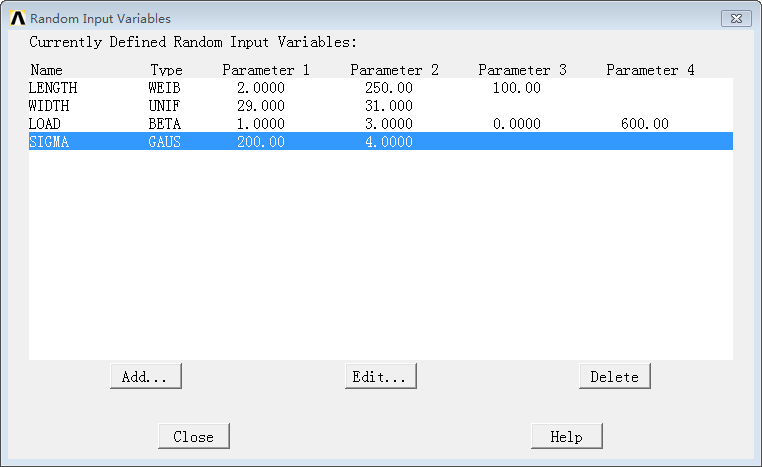
输入变量定义

之后定义输出变量，与输入变量一样，需要名称保持一致，这里使用下面的语句进行定义，或者在GUI中操作。

关于分析方法的定义，本文采用了蒙特卡罗超立方抽样(LHS)方法，由于时间的限制，这里设置抽样次数为100次，其他值设置如图所示：

分析方法定义

执行分析，分析的时间取决于机器的能力以及相应的循环次数，这里设置为100次，速度还可以，需要耐心等待：

循环分析

在计算完成后可以看到结果：

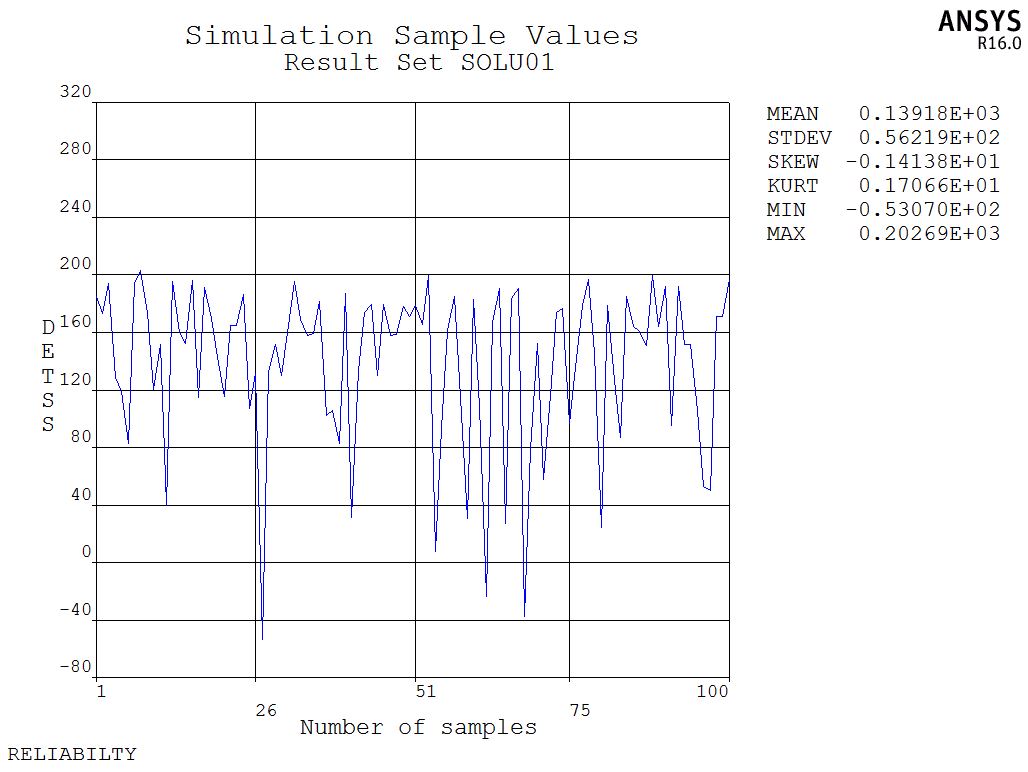
随机输出变量采样

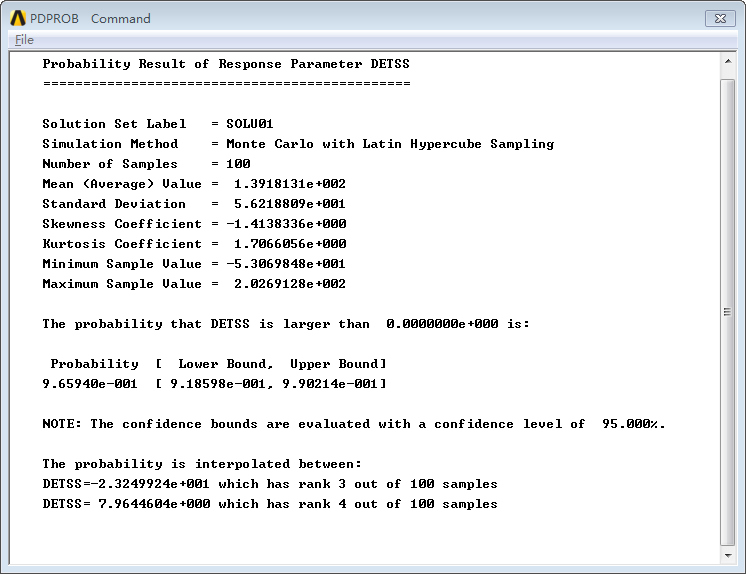
大于0概率

从上图可以看出，扳手不失效的概率在95%的置信度下约为：0.9659。下图在给出随机输入变量和随机输出变量之间的灵敏度系数，以及扳手的长度对输出变量的影响图：

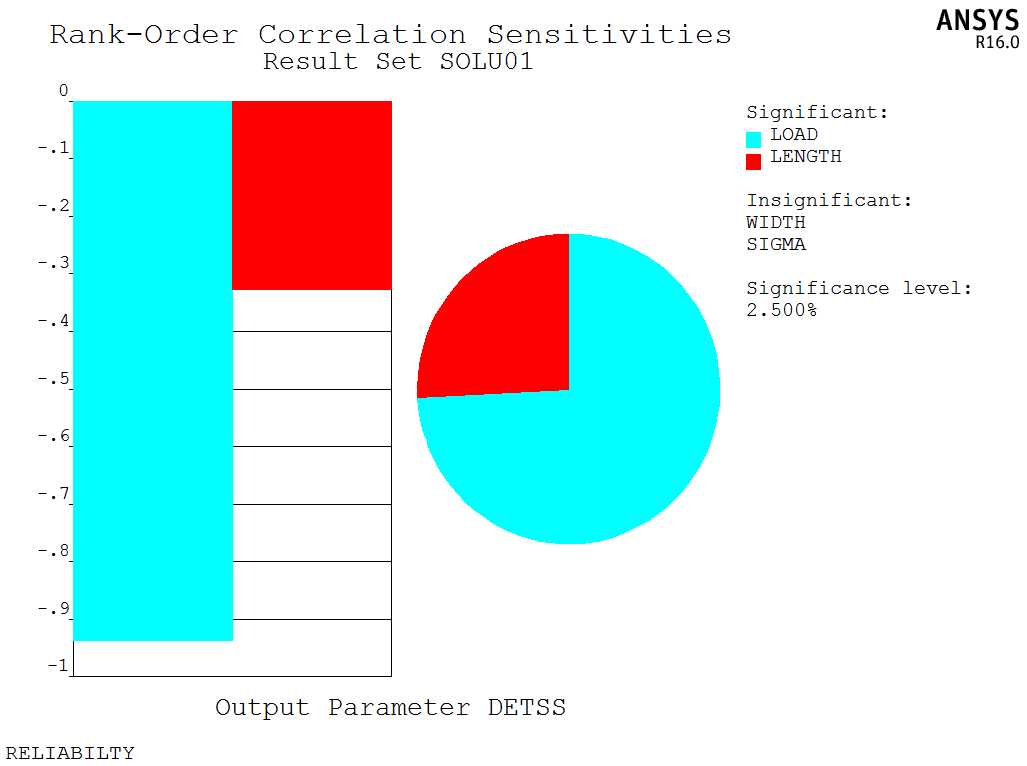
灵敏度关系

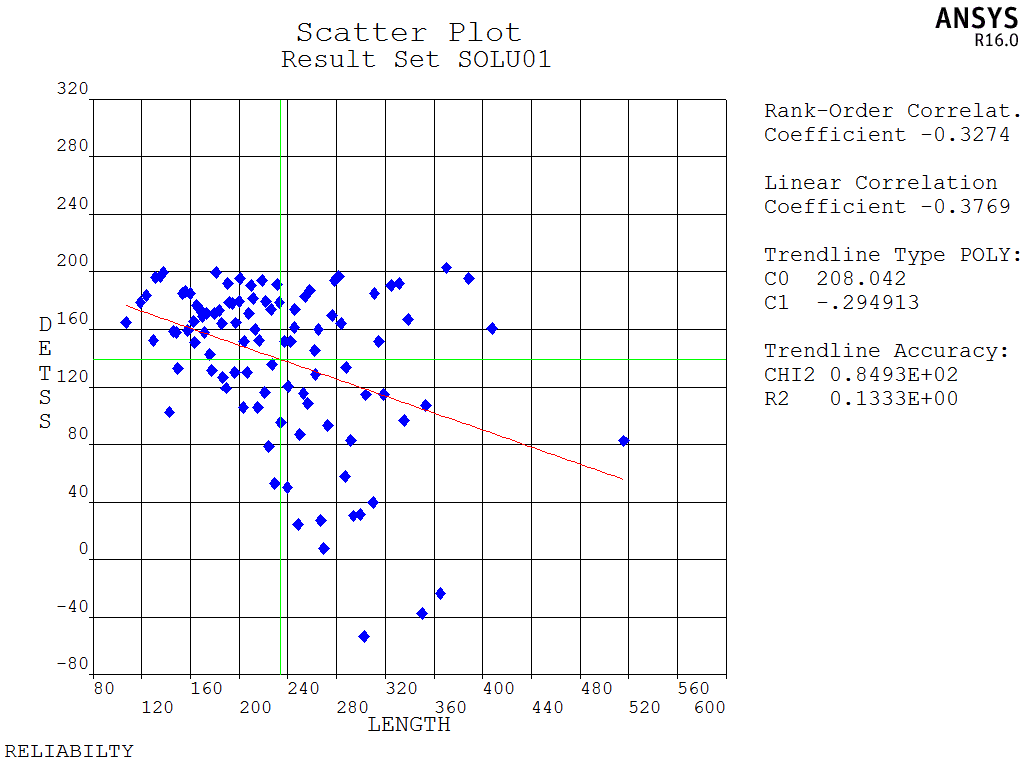
长度的影响

APDL代码如下所示：