在实际工程中,总是存在着各种随机因素,但是在有限元分析中,各种因素都是确定的,杆件截面的尺寸,荷载,弹性模量,密度等等都是固定下来的。而往往这些数值的差异是导致有限元分析结果与实际结构不相同的根本原因。可靠性分析方法就是在分析过程中,根据响应的分布规律,随机设置输入参数的值,从而分析这些数值的变化对所分析结果的影响。进而采用可靠性指标对结果进行评判,从而在不能完全消除参数的不确定性的情况下,提高分析的准确性和设计产品的质量与可靠性。虽然目前解决可靠性分析的方法多种多样,但是实际采用也就是被大家认可的基本上就是蒙特卡罗方法和响应面方法,这些方法在ANSYS中都有相应的模块。

Monte Carlo method
蒙特卡罗模拟技术是最传统也是最常用的分析手段,它能清楚的模拟实际问题的真实行为,一个循环仿真就是一个制造加工零件的过程,在ANSYS中蒙特卡罗方法又可以分为直接抽样和拉丁方法。
蒙特卡罗方法的优点主要如下
- 对有限元模型的适应性好,这主要在于蒙特卡罗方法不需要对模型进行假设,无论什么样的物理模型,都可以进行相应的随机模拟。其分析假设的前提就是确定性模型必须是正确的。在使用蒙特卡罗分析方法时,可不能进行无限多次循环,因此要想使得结果达到一定的可信度,必须要使得在有限多次的分析结果中,能够代表实际的不确定问题,从而确保概率结果具有很高的置信度。
- 蒙特卡罗是概率设计基准和有效性验证的唯一合适方法。
- 蒙特卡罗分析过程所有的循环都是独立的,他们毫不相关,任何一组循环都可以表示真实情况中的一种。
蒙特卡罗直接抽方法
直接抽样法是蒙特卡罗模拟技术中最常用的基本方法,可以直接用于模拟各种行为,非常便于使用。一个循环表示一个零件的生成,但是其并不是最有效的方法,因为直接抽样方法需要大量的循环,效率比较低,随着计算机技术的发展,这些缺点在逐步的被克服。该方法目前已经被广泛的接受,特别是用于抽样基准和有效性验证方面。除此之外,该方法还有一个缺点,就是没有数据记忆功能,这也就意味着它是真正随机的,可能在独立的两次循环中生成相同的输入数据从而导致计算分析效率的降低。
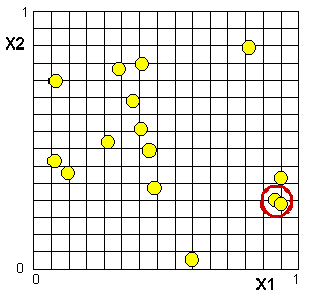
直接抽样法
拉丁超立方抽样
该方法简称为LHS抽样法,这个 方法要比直接抽样法更加高效,同时更加先进。LHS抽样法和直接抽样法的唯一区别就是LHS方法具有记忆功能,也就意味着在实际抽样的过程中可以避免抽取 相同的数据。同时,它强制抽样过程中的数据点必须离散分布在整个抽样空间中。正因为如此,在一般情况下,相同问题要得到相同精度的结果,LHS抽样法比直 接抽样法要少20%~40%循环数量。
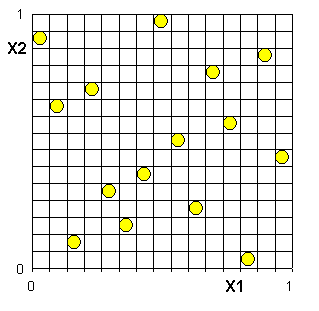
LHS方法
就目前而言,蒙特卡罗随机抽样要想达到理想的结果抽样次数一般在千次以上,需要主意的是ANSYS软件最大抽样只能是5000次,一般2000次的抽样数就可以达到所需要的分析精度。




