之前因为实际需要,根据Mathematica论坛提供的方法,自己手动提取了一下图片的数据,发现确实很好用,而且很智能。其实主要还是MMA比较好用,提供了大量的图像处理函数。我大致看了一下MMA的帮助文档,图像相关的函数应该有上百个,而且还有大量计算机形态学方面的函数,这样可以智能的进行图片处理了,用得好的话,就是一个函数式Photoshop啊。
1.分式线性变换
这里要先说一点变换的知识,当年的代数基本全部还给老师了,折腾了半天弄懂了点东西,赶紧记录一下。
首先是MMA的一个函数LinearFractionalTransform,这个函数的学名叫做分式线性变换,根据维基百科的介绍(可怜的百度百科挫的不行),这个又叫做莫比乌斯变换:
在几何学里, 莫比乌斯变换是一类从黎曼球面映射到自身的函数。
看了这第一句话之后,我后面就没打算看了,有机会去研究研究,但是目前来说开头第一步就卡住了,不是很好,于是我就得直接去看这个MMA帮助,帮助总归是比较通俗易懂一点。
简单来说,这个函数是这样使的:
|
1 |
LinearFractionalTransform[{{{1, 2}, {3, 4}}, {5, 6}, {7, 8}}] |
这样会产生这样一个变换的矩阵:
\[{\rm{TransformationFunction}}\left[ {\left( {\begin{array}{*{20}{c}}
1&2&5\\
3&4&6\\
7&8&1
\end{array}} \right)} \right]\]
其实这个矩阵的变换含义是很清晰的,我们使用x和y进行输入就可以看到:
\[\left\{ {x,y} \right\} \to \left\{ {\frac{{5 + x + 2y}}{{1 + 7x + 8y}},\frac{{6 + 3x + 4y}}{{1 + 7x + 8y}}} \right\}\]
矩阵的第三行作为分母,上面两行分别为作用于x和y进行变换。
其实还可以这么写:
|
1 |
LinearFractionalTransform[{{1, 2, 0}, {3, 4, 0}, {0, 0, 1}}]; |
这样就看的比较明显,在这样的输入下,变换就是:
\[\left\{ {x,y} \right\} \to \left\{ {x + 2y,3x + 4y} \right\}\]
其基本形式就是n空间到m空间的一个变换:
\[\left[ {\begin{array}{*{20}{c}}
1&2\\
3&4
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{x_n}}\\
{{y_n}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{x_m}}\\
{{y_m}}
\end{array}} \right]\]
根据这样一个理论,如果我们要将m空间变换为n空间,只需要获得变换矩阵的逆矩阵就行了。
2.简单例子
上面看起来比较简单,但是实际使用的时候还是比较绕的,我用一个简单的例子来说明一下。用最简单的分式线性变换:
|
1 |
LinearFractionalTransform[{{a, b, 0}, {c, d, 0}, {0, 0, 1}}]; |
我们对直角坐标系下面的两个基向量进行变换:
\[\begin{array}{*{20}{l}}
{\left[ {\begin{array}{*{20}{c}}
a&b\\
c&d
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
0\\
1
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
b\\
d
\end{array}} \right]}\\
{\left[ {\begin{array}{*{20}{c}}
a&b\\
c&d
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
1\\
0
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
a\\
c
\end{array}} \right]}
\end{array}\]
然后我们合并这两个向量得到一个矩阵:
\[\left[ {\begin{array}{*{20}{c}}
a&c\\
b&d
\end{array}} \right]\]
不难发现,如果我们获得m空间的基向量,那么组合并转置之后可以直接取逆变换回去。根据这个简单的例子,我们开始对图形进行恢复。
3.逆矩阵获得
首先还是需要一个透视图,如下图所示:
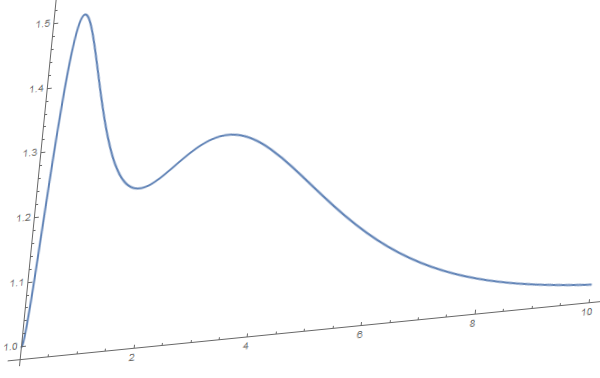
MMA图形变换分析
上面的图片和之前数据提取用的图片是一样的,下面是生成代码:
|
1 2 |
t = LinearFractionalTransform[{{1, 0.1`, 0}, {0.1`, 1, 0}, {0.0, 0.0`,1}}]; img = ImagePerspectiveTransformation[Rasterize[Plot[x^((x - 1)^2 E^-x) + E^-x, {x, 0, 10}, PlotStyle -> Thick], ImageSize -> 600], t, Padding -> White] |
从这个代码可以看出,这个透视变换的变换规则是这样一个矩阵:
\[\left[ {\begin{array}{*{20}{c}}
1&{0.1}\\
{0.1}&1
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{x_n}}\\
{{y_n}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{x_m}}\\
{{y_m}}
\end{array}} \right]\]
现在假设我们不知道这个变换过程。但是有一点是明白的,就是这个图片的两个坐标轴在实际空间是垂直的,那么就可以根据上面的简要思路进行变换。
首先先将坐标轴的数据提取出来,那么我们要用到前文的方法:
|
1 |
brize = Binarize[ColorNegate[img], 0.57] |
先获取图像的负片然后进行二值化处理,设定恰当的阈值0.57,这样就可以获得下面的图片:

MMA图形变换分析
获得这样的图片之后就可以直接使用MMA的ImageLines[ ]函数获得这个图片中的直线的端点,这个图片中有两条直线,可以获得四个点,然后用这些点相减可以获得两个向量,即“图片空间”的一对正交向量。
|
1 2 |
lines = ImageLines[brize]; m = (Subtract @@ Reverse[#]) & /@ lines // MatrixForm |
计算的结果是:
\[\left[ {\begin{array}{*{20}{c}}
{600.}&{59.92}\\
{ – 38.51}&{ – 378.}
\end{array}} \right]\]
通过与原始变换矩阵对比:
\[\left[ {\begin{array}{*{20}{c}}
1&{0.1}\\
{0.1}&1
\end{array}} \right] \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{600.}&{59.92}\\
{ – 38.51}&{ – 378.}
\end{array}} \right]\]
我们可以发现其实存在着倍数的关系,当然由于是图像提取不可能完全的准确,然后还有一条直线的坐标向量是颠倒的,但是这个是没有没有关系的,待会儿可以将图像颠倒一下和这个矩阵做运算:
|
1 2 |
d = DiagonalMatrix[ImageDimensions[img]*{1, -1}]; minv = d.Transpose[Inverse[m]]; |
将图像的尺寸颠倒一下,然后点乘上面的矩阵的转置求逆,这样就获得了逆变换的一个矩阵了:
\[\left[ {\begin{array}{*{20}{c}}
{1.01}&{ – 0.10}\\
{ – 0.10}&{1.01}
\end{array}} \right]\]
4.图像处理
剩下的就比较简单了,首先是和上次一样进行掩膜处理。将刚才获取的线的坐标在图片上面绘制出来,加粗覆盖坐标区域:
|
1 |
mask = Graphics[{Thickness[0.01], Black, Line /@ lines}, Background -> White, PlotRange -> Transpose[{{1, 1}, ImageDimensions[img]}]] |
这样我们可以获得一张坐标轴的遮罩:

MMA图形变换分析
这样用下面的代码对这个遮罩反色,将坐标轴区域设置为感兴趣区域,然后进行这个区域的处理,将这个区域全部去除:
|
1 |
axesFree = ImageMultiply[ColorNegate[img], mask] |
可以得到下面的图片:
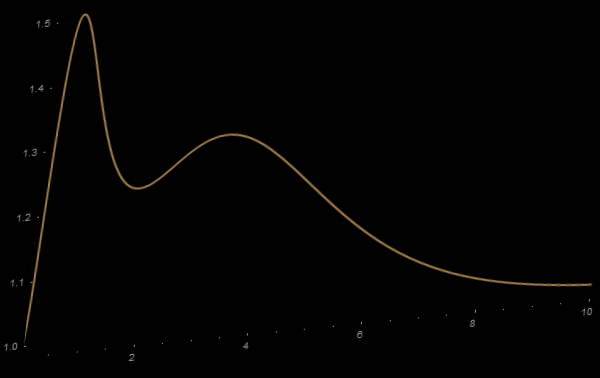
MMA图形变换分析
直接采用刚才计算的逆变换矩阵,使用MMA的透视变换函数进行逆变换:
|
1 |
axesFreeOrig = ImagePerspectiveTransformation[axesFree, minv, Padding -> Black] |
就可以得到一张很正规的图片了:
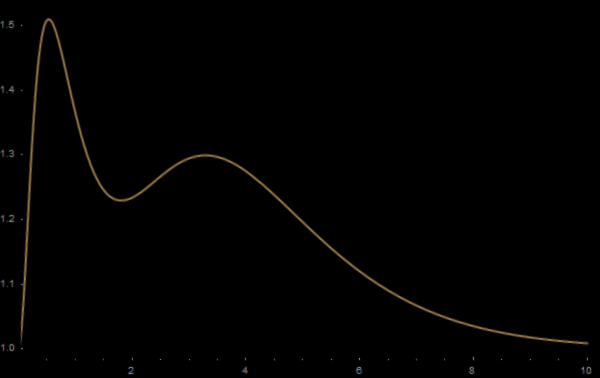
MMA图形变换分析
然后获取图片的形态学分量,并对图片进行细化:
|
1 2 |
comp = MorphologicalComponents[axesFreeOrig]; curve = Thinning[Image[SelectComponents[comp, "Count", -1], "Bit"]] |
图片的曲线将会非常的突出:
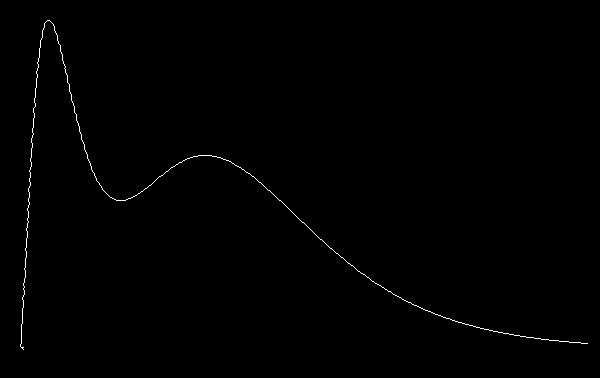
MMA图形变换分析
之后便是点的提取工作了,这和之前的文章内容一样,就不再分析了:
|
1 |
points = #[[First@FindCurvePath[#]]] &@ Position[Transpose@ImageData[curve, "Bit", DataReversed -> True], 1]; |
5.End小结
图像处理真的是涉及到很多的矩阵知识,只是可惜很多都已经还给老师了,有时间还是要补补课的。关于空间映射知识,在课堂上讲真的是非常非常的无聊,如果能够像这样结合点例子,那么讲课也会变得特别有趣。
Anyway,总算是晕晕乎乎的写完了,也不知道其中有多少问题。这个东西还是蛮实用的,所以就留下来以供以后参考参考。
给出一个文中代码的下载链接:LI87N9.zip
最后感谢一下文末的网站内容作者,专业的MMA论坛,非常厉害啊!




