一直感觉图像处理是个复杂的学科,也一直没有机会学,直到有了一点实际需求。在实际分析和写论文的过程中,经常需要一些论文和试验数据,如果是自己的数据也就算了,但是有很多是别人论文里面的数据,但是去要原始数据又不是很好。因此我们需要一些方法去提取试验数据。
目前而言,对于需要提取数据只能是靠手动拟合,换句话说,如果需要别人试验的数据作为自己的输入参数的话,只能是手动去在图像上点。当然如果是用自己的结果和别人的数据去比对的话,则简单一些。下面就来说说从图像中提取数据,顺便学习学习MMA。
1.思路分析
其实如果不是获取数据用于模型分析的话,还是比较简单的。目前已经有很多的人开发了这种或者那种的软件,其基本思路也都是一致的。如果换做是我们进行处理,那我们处理的手段也是很多的。最简单的可以采用下面的思路进行获取:
- 获取坐标数据;
- 分析曲线颜色;
- 将图形分块;
- 按照每一块的平均颜色与要获得的颜色对比;
- 在容差范围内则记录坐标;
这样的处理方式是最常见也是最普遍的,对于一张普通的图片,采用上面的方法可以有效地提取图片的数据点,例如下面这张图片就可以这样处理:
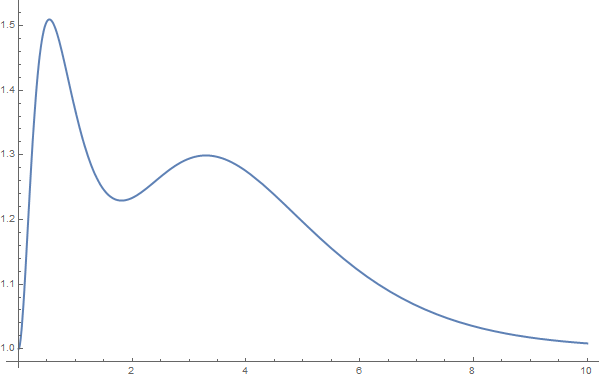
MMA图片数据提取
但是如果是下面一张图的话,那么上面的思路是行不通的:
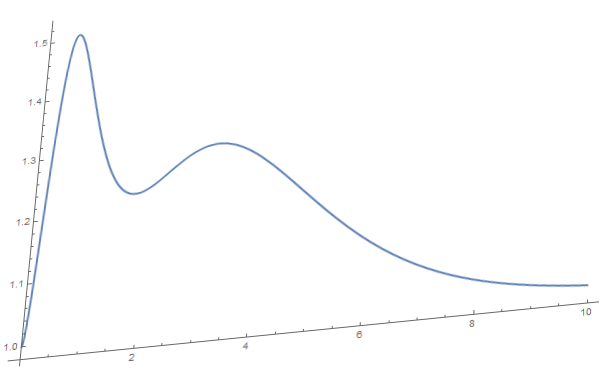
MMA图片数据提取
因为这张图是一张透视图,这样的话按照上面获得的数据是完全错误的,但这种情况确是常见的。当我们从原文传递的论文中处理图片数据的时候,基本上都是这种带有一点透视关系的曲线。于是怎么从这样的曲线中提取出我们想要的数据,便是一个挑战。
这个图片采用一般的分析思路是不行的了,必须要采用一些专用的软件进行处理,这里使用的是Mathematica,是我比较喜欢的工具,另外就是这个方法是在MMA的论坛上发现的,因此这里简单分析一下。顺便好久不用了,复习一下MMA的使用方法。
2.图形分析
首先我们发现这张图是一张透视图,在原图和这张图之间存在这透视变换,因此我们需要找到这样一个透视变换关系。 MMA为我们提供了一个很有用的函数FindGeometricTransform,这个函数是用来获得一个几个变换函数的,根据MMA的帮助文档:
|
1 2 |
FindGeometricTransform[pts1,pts2] 求将由pts2指定的位置与 ts1对齐的几何变换,返回对齐误差以及变换函数. |
因此我们现在这个图像想选择一些实际数据点,这里我选择了{0, 1.0}, {0, 1.5}, {10, .98}这三个点,然后我们获得这三个实际数据点在图中的像素坐标位置,这个可以先用Import[ ]这个函数将图片导入进来,然后右键图片,选择获取坐标选项,点击这三个点在图片上的位置,然后Ctrl+C获得这三个点的像素坐标。这里的像素坐标是:
|
1 |
{o, y, x} = {{20.56, 31.74}, {50.31559963931469, 334.72}, {587.02, 75.03}}; |
直接将其赋值给三个坐标变量;
然后可以使用FindGeometricTransform获得其几何变换:
|
1 |
trans = FindGeometricTransform[{{0, 1.0}, {0, 1.5}, {10, .98}}, {o, y, x}][[2]] |
这里要注意的是这个变换函数会返回误差和变换函数,因此这里用[[2]]获得其变换函数。这样我们可以通过这个变换函数作用于提取出来的数据转换成实际的坐标数据了。
3.颜色处理
获得变换坐标之后就可以着手进行数据提取了,数据提取需要的是一个干净的图像,因此我们可以手动将图片进行处理,也可以让MMA自动对这个图片进行处理。
在这之前先了解一下颜色的构成,按照颜色的规范化光栅数据,对于黑白来说0表示黑色,1表示白色。同样对于RGB的基本色来说,存在下面的对应关系:
|
1 2 |
{0,0,0}=>黑色; {1,1,1}=>白色; |
其他颜色均在这二者之间,因此首先进行颜色标准化处理,采用round[ ]函数:
|
1 |
data = Round[ImageData[img], 1]; |
这里的img就是import进来的图片了。上面的操作将图片中的所有颜色的RGB分量全部四舍五入成1的倍数,即RGB分量要么是0,要么是1。图片会变成下图所示的样子。
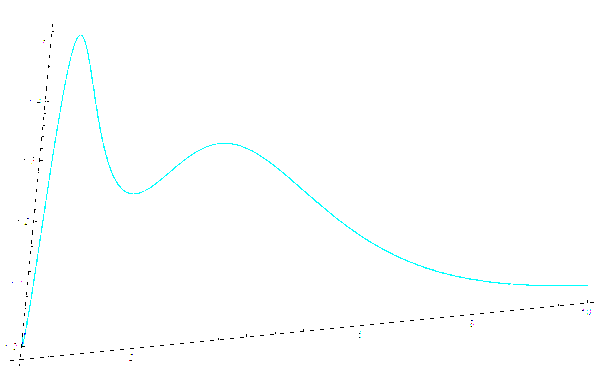
MMA图片数据提取
这时候的data是一个三维矩阵,因为除了图片的二维之外,每个点还有三个颜色数据,将其中的重复数据删除之后,用Graphics[ ]命令将图像绘制成圆盘格式查看:
|
1 2 |
col = DeleteDuplicates[Flatten[data, 1]]; Graphics[{RGBColor[#], Disk[]}, ImageSize -> Tiny] & /@ col |

MMA图片数据提取
可以发现曲线对应的颜色就是第三个圆盘对应的颜色,第一个圆盘是白色的所以看不见。这样我们就可利用颜色替换的方式,保留{0,1,1}颜色,即第三个圆盘的亮蓝色。其他颜色全部用0代替,即用黑色填充。
|
1 |
binImage = Image@Replace[data, {col[[3]] -> 1, _ :> 0}, {2}] |
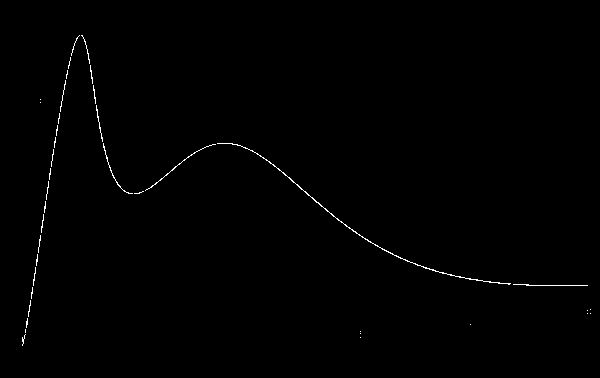
MMA图片数据提取
但是这样还是会发现这张图中存在一点问题,就是坐标轴的位置还是有白色。这时候一串图形处理模式就用上来了,首先进行高斯滤波,去除这个白点,并用二值化扣出图像中的黑色部分:
|
1 |
lpic = Binarize[GaussianFilter[binImage, 5]] |
这样我们可以得到下面的图片:

MMA图片数据提取
这张图片干净了很多,然后我们打算进行掩膜处理,就是一个遮罩,但在进行处理之前我们还需要进行反色用以获取感兴趣的区域:
|
1 |
pic = ColorNegate[lpic] |
这样我们得到感兴趣的白色区域:

MMA图片数据提取
上面这张图只是一个类似于遮罩的东西,白色表示我们要处理的区域,黑色表示保护区域,这样我们采用函数对图像操作时,黑色部分将会被保护,也就是我们的那条细细的数据线会被保护。
|
1 |
curve = ImageApply[{0, 0, 0} &, binImage, Masking -> pic] |
通过上面的代码,将binImage这个图片用黑色填充,当然这是在有保护的情况下进行的,这样就可以得到下面的清晰的数据图了:
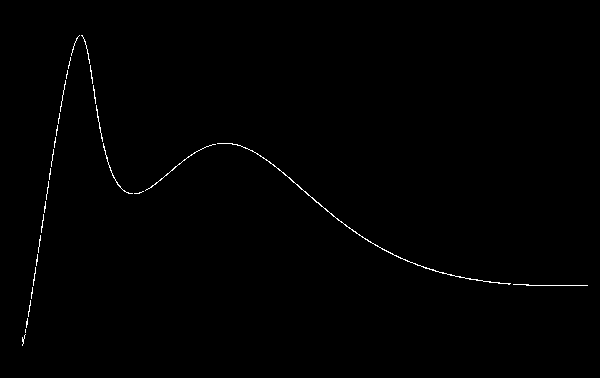
MMA图片数据提取
4.数据提取
获得上面的这张图之后,剩下的就好做了,用Position[ ]函数直接提取图片中的白色像素点,然后通过几何变换函数将提取的像素坐标变换成实际的坐标即可:
|
1 2 |
curvLoc = (Reverse /@ Position[ImageData[curve, DataReversed -> True], {1., 1., 1.}]); Show[ListPlot[trans /@ curvLoc, PlotRange -> All], plot] |
然后我们可以和没有变形之前的图片对比一下:
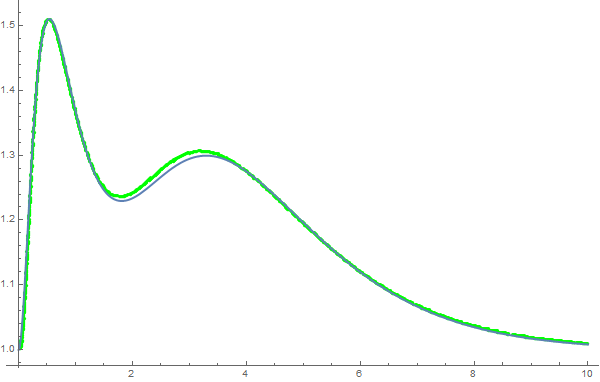
MMA图片数据提取
5.End小结
虽然这个方法不是我的,但是看懂了确实挺费劲的,好久没用MMA加上一串各种缩写,看的也是头晕眼花的,不过还好,花了点时间看懂了。趁我还能看懂的时候赶紧将这个写下来,不然以后又要忘掉了。
给出一个文中代码的下载链接:KV96P5.zip
最后还是感谢一下MMA论坛的高手们,看得懂和想得到还是两码事的。




