在对数据进行处理的过程中,需要对数据规约。当数据量特别庞大的时候,就需要采用更高效的方式进行处理。数据规约可以将有效地减小所需分析的数据量,提高分析效率。
数据规约可以删除不需要或者不相关的数据,降低数据位数,提高数据分析的效率。数据规约用于寻找最小属性子集,并确保新的数据子集的概率分布尽可能接近原来的数据的概率分布。
这个描述不是很好理解,其实就是采用较为简单的方式对大量数据进行归类和分析,从而简化数据分析工作。而对于主成分分析(PrincipalComponents)其实就是将大量数据中相关性较高的变量转换为彼此相互独立或者不相关的变量。
主成分分析经常用于减少数据集的维数,同时保持数据集中的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是,这也不是一定的,要视具体应用而定。由于主成分分析依赖所给数据,所以数据的准确性对分析结果影响很大。
要实现主成分分析的计算,必须要了解一下计算原理和实现方法。
1.计算实现
根据维基百科介绍:
PCA的数学定义是:一个正交化线性变换,把数据变换到一个新的坐标系统中,使得这一数据的任何投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。
这个比较复杂,我直接从书中找来一个计算流程:
- 设定原始变量\({X_1},{X_2}, \cdots ,{X_P}\)的\(n\)次观察数据矩阵为:
\[X = \left[ {\begin{array}{*{20}{c}}
{{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1p}}}\\
{{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2p}}}\\
\vdots & \vdots & \vdots & \vdots \\
{{x_{n1}}}&{{x_{n2}}}& \cdots &{xnp}
\end{array}} \right] = \left( {{X_1},{X_2}, \cdots ,{X_P}} \right)\]
- 数据进行标准化处理,由于数据是按列记录的,因此需要按列进行标准化处理:
\[{x^*} = \frac{{x – \overline x }}{\sigma }\]
- 计算相关系数矩阵\(R\),\(R = {\left( {{r_{ij}}} \right)_{p \times p}}\),其中\({{r_{ij}}}\)由下式定义:
\[{r_{ij}} = \frac{{\sum\limits_{k = 1}^n {\left( {{x_{ki}} – \overline {{x_i}} } \right)\left( {{x_{kj}} – \overline {{x_j}} } \right)} }}{{\sqrt {\sum\limits_{k = 1}^n {{{\left( {{x_{ki}} – \overline {{x_i}} } \right)}^2}\sum\limits_{k = 1}^n {{{\left( {{x_{kj}} – \overline {{x_j}} } \right)}^2}} } } }}\]
其中\({{r_{ij} = r_{ji}}}\),且\({r_{ii}} = 1\)。
- 求解\(R\)的特征根并按照从大到小的顺序排列:\({\lambda _1} \ge {\lambda _2} \ge {\lambda _p} > 0\)
- 确定主成分个数\(m\):
\[\frac{{\sum\limits_{i = 1}^m {{\lambda _i}} }}{{\sum\limits_{i = 1}^p {{\lambda _i}} }} \ge \alpha \]
其中\(\alpha \)根据实际问题确定,取值一般为80%。
- 计算\(m\)个相应的特征向量:
\[\beta = [{\beta _1},{\beta _1}, \cdots ,{\beta _m}]\]
- 计算主成分:
\[Z = X\beta \]
这样就可以计算得到相应主成分矩阵了。
2.MMA实现
根据计算原理,首先需要将导入的数据计算每一列的标准差和平均值:
|
1 2 3 4 |
Clear["Global`*"]; data = Flatten[Import[NotebookDirectory[] <> "component.xls"], 1]; columnMean = Mean /@ Transpose[data]; columnDeviation = StandardDeviation /@ Transpose[data]; |
计算平均值和标准差的过程中,由于映射函数对于二维矩阵只能以行向量的方式进行计算,因此需要进行转置。计算完成之后进行数据矩阵的标准化:
|
1 2 |
tdata = Transpose[data]; data = Transpose[Table[(tdata[[i]] - columnMean[[i]])/columnDeviation[[i]], {i, Length[tdata]}]]; |
同样出于快速标准化的要求,需要先将数据矩阵转置后,进行行操作,然后计算获得结果之后再转置回来,这样可以得到标准化之后的矩阵。
相关系数求法可以直接采用相关函数计算矩阵的协方差矩阵:
|
1 |
corrM = Correlation[data]; |
计算完成之后,获取协方差矩阵的特征值并进行阈值控制:
|
1 2 3 4 5 6 |
eigV = Eigenvalues[corrM]; accV = Accumulate[eigV]/Total[eigV]; m = 0; For[i = 1, i <= Length[accV], i++, If[accV[[i]] > 0.80, m = i; Break[], Continue[]]; ]; |
这里采用了累加函数,当阈值大于80%的时候保存位置,并跳出循环。在完成这一步之后,便可以进行主成分矩阵的合成:
|
1 2 3 |
eigE = Eigenvectors[corrM]; eigM = Transpose[Table[eigE[[i]], {i, m}]]; zZ = data.eigM // MatrixForm |
计算到这里\(zZ\)即为主成分。
3.实例验算
这里采用一个小的数据矩阵进行实际验算,数据矩阵如下图所示:

MMA实现主成分分析
为了保留更多的信息,这里将阈值由80%调整为97%后进行计算,可以得到下面的主成分部分:
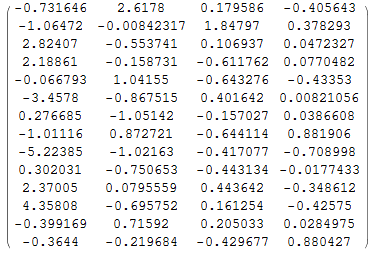
MMA实现主成分分析
为了验证正确性,我们直接使用MMA自带的主成分计算函数进行一次计算:
|
1 |
PrincipalComponents[N[data]] // MatrixForm |
可以得到下面的主成分部分:
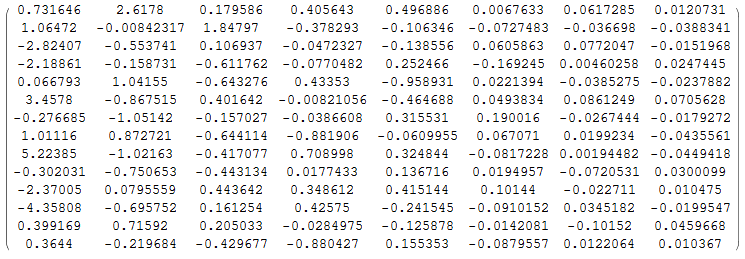
MMA实现主成分分析
可以发现计算结果是一致的。
4.MMA自带函数
其实除了主成分计算函数PrincipalComponents[ ]外,MMA也还有其他的一些比较有用的函数,比如:
|
1 |
Transpose[Standardize[Transpose[data]]] |
采用Standardize[ ]函数可以直接对数据矩阵进行标准化,但是需要注意的是,这个Standardize[ ]函数在进行标准化之后,会对标注化结果进行转置,所以在前面增加一个转置函数转置回来。
5.End小结
有人会觉得本来在MMA中就是一句话的事,非要弄得这么复杂,这样是否有必要。正好我看到一句知乎名言用来回答一下:
要有造轮子的能力和不重复造轮子的觉悟。
最后还是感谢一下文末的参考文献的作者们。
给出一个文中代码的下载链接:IF98v4.zip
6.Reference
- 廖芹. 数据挖掘和数学建模[M]. 北京: 国防工业出版社. 2010.
- 张良均, 王路, 谭力云,等. Python数据分析与挖掘实战[M]. 北京: 机械工业出版社. 2016.




