在结构分析的过程中,往往是多种单元一起使用,不可避免的涉及到单元之间的连接问题。常用的单元如梁、壳和实体单元一般采用共节点的方式进行连接,由于单元之间自由度的差异,这样的连接得不到想要的结果,甚至会形成机构而不收敛,因此在不同单元之间设置必要的“协调条件”不可少。
约束方程是构建“协调条件”的一种常用手段,其基本形式如下所示:
\[Constant = \sum\limits_{I = 1}^N {\left( {Coeff\left( I \right) \times U\left( I \right)} \right)} \]
其中:U(I)为自由度项;Coeff(I)为自由度U(I)的系数;N为方程中项的编号。
对于约束方程的施加,在ANSYS中可以使用CE命令,其基本形式如下:
CE, NEQN, CONST, NODE1, Lab1, C1, NODE2, Lab2, C2, NODE3, Lab3, C3
其中:
NEQN为约束方程编号,可取值为:
=N:任意编号;
=HIGH:既有约束方程的最高编号,这个非常适用于向已有的方程中增加自由度;
=NEXT:既有约束方程最高编号+1,自动编号选项;
默认为HIGH。
CONST为方程的常数项Constant;
NODE1为约束方程的第一项的节点号,如果使用-NODE1则为删除该项;
Lab1为第一项的节点自由度标识符,可以用UX、UY、UZ、ROTx、ROTy、ROTz进行表示;
C1为第一项系数,如果设置为0则不计入该项。
其他选项与上述类似,当约束方程的项数多于三项时,可以重复执行该命令,使用默认的HIGH向该方程中增加其他项;如果修改约束方程的常数项,则采用不带节点参数的CE命令,求解期间也只能修改约束方程常数项,可以使用CECMOD命令。
下面分析一个具体的问题,模型如下图所示:对于该模型,节点5虽然为公用节点,但是两端的弯矩与实体单元的弯矩并不耦合,因此需要人为的构建约束方程,现假定实体单元划分为四份,连接面的节点编号如上图所示,根据约束方程的定义,需要为此模型定义三个约束方程用以控制三个方向的自由度,下面给出一个5号节点ROTz约束方程示例:
\[\frac{{U{X_2} – U{X_1}}}{{D{y_{2 – 1}}}} = – ROT{z_5}\]
该方程根据1、2节点的水平和竖向位移差值之比定义5节点ROTz的转动自由度,因此约束方程可以改写为标准方程:
\[0 = U{X_2} – U{X_1} + ROT{z_5} \times D{y_{2 – 1}}\]
采用ANSYS命令流表示为:
CE,1,0,2,UX,1,1,UX,-1,5,ROTZ,NY(2)-NY(1)
在实际模型中,如果不确定具体的节点编号可以使用内置函数命令NNEAR获取最近节点即可,相应的有限元模型如下图所示:
有限元模型
模型建立后,定义相应的节点约束方程,本模型中定义了中心节点三个方向的约束方程,方程定义采用上述的方法,定义完成如下图所示:

耦合设置
施加荷载并求解,可以看出在定义了约束方程的模型中分析正常,下图给出了梁的弯矩图与理论分析一致:
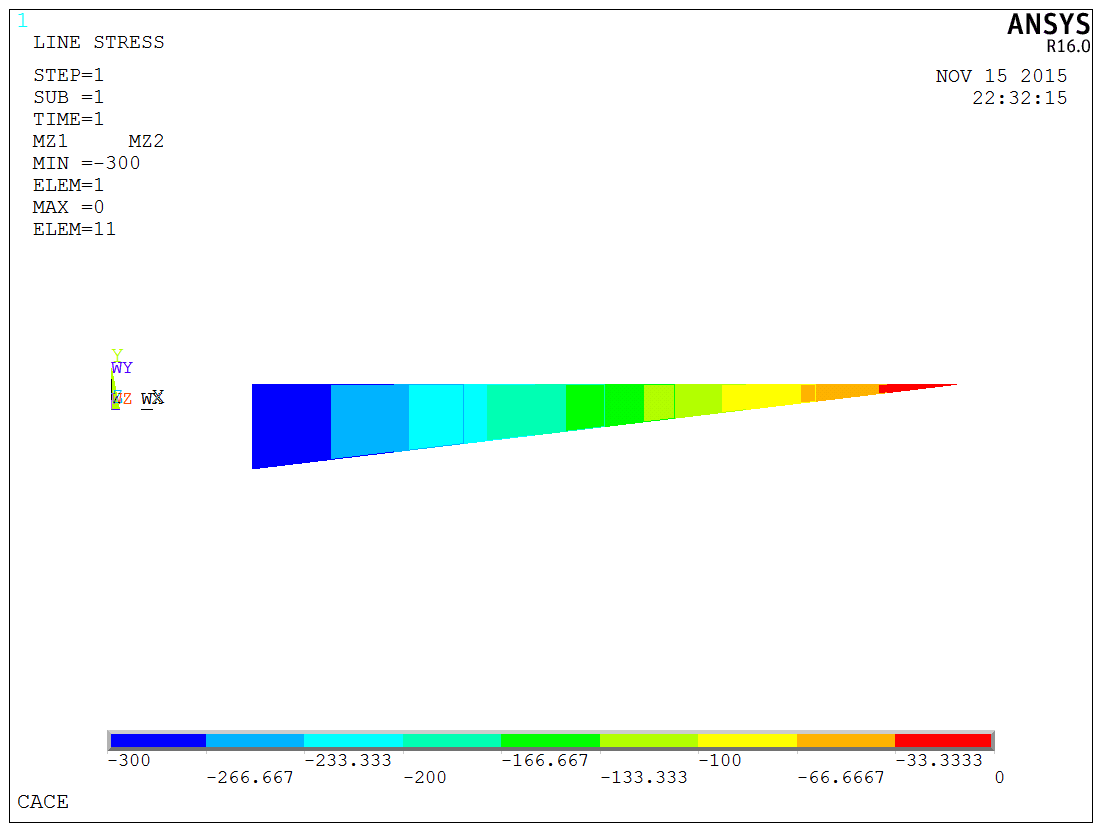
梁端弯矩图
APDL代码以如下所示:




