上次采用过Mathematica自带的微分方程求解器求解,虽然求解的精度非常的不错,但是求解的速度非常慢。为了提高地震波反应谱的计算速度,并且能够同时计算不同阻尼比下的多个反应谱,需要一种新的计算方法。目前基本的就是NewMark法,但是这次给出的是一个比较常规的递推算法。这种方法计算简单,计算效率比较高,且同时给出了位移谱、速度谱和加速度谱。
1.基本知识
对于结构动力响应的计算,如果采用Duhamel积分,那么计算效率是比较低下的,即便是对于简单的荷载形式,在采用Duhamel积分也是非常的复杂。而地震波往往是没有规律的,不能表述为简单的数学表达式,即便是像以前那样采用插值函数进行表达,计算效率也是比较低下的。因此,考虑到实用性方面,必须要采用数值方法对地震响应进行计算。
有两种方法可以进行地震响应的数值计算:
- 地震波插值计算
- 数值积分计算
这两个方法对于线性系统都是适用的,但是对于非线性系统只有第二个方法有用。
2.时间步进法
根据结构动力学书上的方法,可以采用时间步进的方式对微分方程进行求解,基本方式如下。
在地震作用下,单自由度体系的基本方程为:
\[m\ddot u + c\dot u + ku = p(t)\]
或者
\[m\ddot u + c\dot u + ku = – m{u_g}(t)\]
上述方程的初始条件为:
\[\begin{array}{l}
\dot u(0) = 0\\
u(0) = 0
\end{array}\]
则在\(i\)时刻结构动力方程为:
\[{m{{\ddot u}_i} + c{{\dot u}_i} + k{u_i} = {p_i}}\]
那么现在就需要找到一种递推方法,可以使得用这种方法递推得到的\(i+1\)时刻的位移、速度和加速度满足下式:
\[{m{{\ddot u}_{i + 1}} + c{{\dot u}_{i + 1}} + k{u_{i + 1}} = {p_{i + 1}}}\]
如果这种递推方法对于所有的\(i=0,1,2…\)均成立的话,那么这种方法就可以作为计算反应谱的一种手段了。
3.外荷载插值
为寻找这样一种递推方法,我们假定\(i\)时刻的外荷载为\(F_i\),则\(\tau \)时刻\((i < \tau \le i + 1)\)的荷载\(F(\tau)\)为:
\[F\left( \tau \right) = {F_i} + \left( {\frac{{\Delta {F_i}}}{{\Delta t}}} \right)\tau \]
其中:
\[\begin{array}{l}
\Delta {F_i} = {F_{i + 1}} – {F_i}\\
\Delta t = {t_{i + 1}} – {t_i}
\end{array}\]
则\(F(\tau)\)即为\(0\)到\(\Delta t\)的插值力。
对于单自由度无阻尼体系,运动方程可以写为:
\[\ddot u + \omega _n^2u = \frac{1}{m}\left[ {{F_i} + \left( {\frac{{\Delta {F_i}}}{{\Delta t}}} \right)\tau } \right]\]
上式由通解和特解进行叠加。通解即为\(\tau =0\)时刻初始状态为\({u_i}\)和\({{\dot u}_i}\)的解,而特解则由两部分组成:
1. 有荷载\({F_i}\)造成的响应;
2. 由\({\left( {\frac{{\Delta {F_i}}}{{\Delta t}}} \right)\tau }\)造成的响应;
因此可以得到:
\[{u_{i + 1}} = {u_i}\cos ({\omega _n}\Delta t) + \left( {\frac{{{{\dot u}_i}}}{{{\omega _n}}}} \right)\sin ({\omega _n}\Delta t) + \frac{{{F_i}}}{k}\left[ {1 – \cos ({\omega _n}\Delta t)} \right] + \left( {\frac{{\Delta {F_i}}}{k}} \right)\left( {\frac{1}{{{\omega _n}\Delta t}}} \right)\left[ {{\omega _n}\Delta t – \sin \left( {{\omega _n}\Delta t} \right)} \right]\]
\[\frac{{{{\dot u}_{i + 1}}}}{{{\omega _n}}} = – {u_i}\sin ({\omega _n}\Delta t) + \left( {\frac{{{{\dot u}_i}}}{{{\omega _n}}}} \right)\cos ({\omega _n}\Delta t) + \frac{{{F_i}}}{k}\sin ({\omega _n}\Delta t) + \left( {\frac{{\Delta {F_i}}}{k}} \right)\left[ {1 – \cos \left( {{\omega _n}\Delta t} \right)/{\omega _n}\Delta t} \right]\]
带有阻尼体系的的递推表达式可以由同样的方式计算得到。下面将用一个更加简单的方式进行表达:
\[\begin{array}{l}
{u_{i + 1}} = a{u_i} + b{{\dot u}_i} + c{F_i} + d{F_{i + 1}}\\
{{\dot u}_{i + 1}} = {a_1}{u_i} + {b_1}{{\dot u}_i} + {c_1}{F_i} + {d_1}{F_{i + 1}}
\end{array}\]
式中:
\[a = {e^{ – \rho {\omega _n}\Delta t}}\left( {\rho \sin {\omega _d}\Delta t + \sqrt {1 – {\rho ^2}} \cos {\omega _d}\Delta t} \right)/\sqrt {\left( {1 – {\rho ^2}} \right)} \]
\[b = {e^{ – \rho {\omega _n}\Delta t}}\left( {\frac{1}{{{\omega _d}}}\sin {\omega _d}\Delta t} \right)\]
\[c = \frac{1}{{k{\omega _n}\Delta t}}\left\{ {2\rho + {e^{ – \rho {\omega _n}\Delta t}}{\omega _n}\Delta t\kappa } \right\}\]
\[\kappa {\rm{ = }}\left[ {\left( {\frac{{1 – 2{\rho ^2}}}{{{\omega _d}\Delta t}} – \frac{\rho }{{\sqrt {1 – {\rho ^2}} }}} \right)\sin {\omega _d}\Delta t – \left( {1 + \frac{{2\rho }}{{{\omega _n}\Delta t}}} \right)\cos {\omega _d}\Delta t} \right]\]
\[d = \frac{1}{{k{\omega _n}\Delta t}}\left\{ {{\omega _n}\Delta t – 2\rho + {e^{ – \rho {\omega _n}\Delta t}}{\omega _n}\Delta t\left[ {\left( {\frac{{2{\rho ^2} – 1}}{{{\omega _d}\Delta t}}} \right)\sin {\omega _d}\Delta t + \left( {\frac{{2\rho }}{{{\omega _n}\Delta t}}} \right)\cos {\omega _d}\Delta t} \right]} \right\}\]
\[{a_1} = – {e^{ – \rho {\omega _n}\Delta t}}\left( {\frac{{{\omega _n}}}{{\sqrt {1 – {\rho ^2}} }}\sin {\omega _d}\Delta t} \right)\]
\[{b_1} = – {e^{ – \rho {\omega _n}\Delta t}}\left( { – \rho \sin {\omega _d}\Delta t + \sqrt {1 – {\rho ^2}} \cos {\omega _d}\Delta t} \right)/\sqrt {\left( {1 – {\rho ^2}} \right)} \]
\[{c_1} = \frac{1}{{k\Delta t}}\left\{ { – 1 + {e^{ – \rho {\omega _n}\Delta t}}\left[ {\left( {\frac{{{\omega _n}\Delta t}}{{\sqrt {1 – {\rho ^2}} }} + \frac{\rho }{{\sqrt {1 – {\rho ^2}} }}} \right)\sin {\omega _d}\Delta t + \cos {\omega _d}\Delta t} \right]} \right\}\]
\[{d_1} = \frac{1}{{k\Delta t}}\left\{ {1 – {e^{ – \rho {\omega _n}\Delta t}}\left[ {\frac{\rho }{{\sqrt {1 – {\rho ^2}} }}\sin {\omega _d}\Delta t + \cos {\omega _d}\Delta t} \right]} \right\}\] 根据上面的递推关系式,并结合初始状态的位移和速度为0,则可以计算每一个时刻的位移和速度。
4.MMA实现反应谱计算
根据上面的分析,只需要将初始的位移和速度作为初始值,可以计算出位移和速度曲线。获取最大值,并存入数组就可以得到反应谱。
首先将地震波导入,并对存放位移、速度和加速度的数组进行初始化,然后需要将地震波的长度和时间间隔提取出来:
|
1 2 3 4 5 6 7 8 9 |
Clear["Global`*"]; de = Import[NotebookDirectory[] <> "elcentro.dat"]; u = Table[0, Length[de]]; v = Table[0, Length[de]]; ta = Table[0, Length[de]]; tt = Length[de]*0.02; n = Length[de]; n1 = Length[de]; dt = tt/n; |
然后将地震波转换一下,将单位g转换为标准的国际单位制,并初始化阻尼和采样的间隔,然后将存放位移、速度和加速度最大值的数值根据采样点数目初始化。简单来说,取样200次,间隔0.05s,就意味着计算周期的范围为0-10s,每个0.05s计算一条位移、速度和加速度的曲线,并获取最大值保存到dmf、vmf和amf数组中去:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
mass = 1; ug = Table[0, Length[de]]; p = Table[0, Length[de]]; For[i = 1, i <= n1, i++, ug[[i]] = de[[i, 2]]; ug[[i]] = -ug[[i]]*9.81; p[[i]] = ug[[i]]*mass; ] (*damper ratio*) rho = {0.00, 0.01, 0.02, 0.05, 0.10, 0.20}; (*sample points and sample time*) bbc = 200; bbt = 0.05; dmf = Table[0, bbc, Length[rho]]; vmf = Table[0, bbc, Length[rho]]; amf = Table[0, bbc, Length[rho]]; |
下面就是主要的循环了,这里对于每一个阻尼的每一个采样点都要进行一次完整的时程计算,计算完成之后获取峰值数值并保存,那么这里计算的6个阻尼就需要总共循环1200次,每次循环需要计算Elcentro地震波的1560个点的位移、速度和加速度:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
For[jj = 1, jj <= Length[rho], jj++, r = rho[[jj]]; mass = 1; ss = Table[0, bbc]; For[ii = 1, ii <= bbc, ii++, tn = bbt*ii; wn = 2.0*Pi/tn; ss[[ii]] = tn; k = mass*wn^2; c = 2.0*r*Sqrt[k*mass]; wd = wn*Sqrt[1 - r^2]; a = Exp[-r*wn*dt]*(r*Sin[wd*dt]/Sqrt[1 - r^2] + Cos[wd*dt]); b = Exp[-r*wn*dt]*(Sin[wd*dt])/wd; c2 = ((1 - 2*r^2)/(wd*dt) - r/Sqrt[1 - r^2])*Sin[wd*dt] - (1 + 2*r/(wn*dt))*Cos[wd*dt]; c = (1/k)*(2*r/(wn*dt) + Exp[-r*wn*dt]*(c2)); d2 = Exp[-r*wn*dt]*((2.0*r^2 - 1)/(wd*dt)*Sin[wd*dt] + 2.0*r/(wn*dt)*Cos[wd*dt]); d = (1/k)*(1 - 2.0*r/(wn*dt) + d2); ad = -Exp[-r*wn*dt]*wn*Sin[wd*dt]/(Sqrt[1 - r^2]); bd = Exp[-r*wn*dt]*(Cos[wd*dt] - r*Sin[wd*dt]/Sqrt[1 - r^2]); c1 = Exp[-r*wn*dt]*((wn/Sqrt[1 - r^2] + r/(dt*Sqrt[1 - r^2]))*Sin[wd*dt] + Cos[wd*dt]/dt); cd = (1/k)*(-1/dt + c1); d1 = Exp[-r*wn*dt]*(r*Sin[wd*dt]/Sqrt[1 - r^2] + Cos[wd*dt]); dd = (1/(k*dt))*(1 - d1); For[m = 2, m <= n1, m++, u[[m]] = a*u[[m - 1]] + b*v[[m - 1]] + c*p[[m - 1]] + d*p[[m]]; v[[m]] = ad*u[[m - 1]] + bd*v[[m - 1]] + cd*p[[m - 1]] + dd*p[[m]]; ta[[m]] = (-c*v[[m]] - k*u[[m]])/mass; ]; dmf[[ii, jj]] = Max[Abs[u]]; vmf[[ii, jj]] = Max[Abs[v]]; amf[[ii, jj]] = Max[Abs[ta]]; ]; ]; |
在保存反应谱的数值后,就可以采用下面的命令将图片绘制出来了,这里我采用的是600像素宽度的曲线,然后图例的位置放置在图片中,可能随着不同计算机的显示位置可能会有偏差:
|
1 2 3 |
ListLinePlot[Transpose[{Table[i, {i, bbt, bbc*bbt, bbt}], Transpose[dmf][[#]]}] & /@ {1, 2, 3, 4, 5, 6}, PlotRange -> All, Frame -> True, GridLines -> Automatic, ImageSize -> 600, PlotLegends -> Placed[rho, {0.1, 0.8}]] ListLinePlot[Transpose[{Table[i, {i, bbt, bbc*bbt, bbt}], Transpose[vmf][[#]]}] & /@ {1, 2, 3, 4, 5, 6}, PlotRange -> All, Frame -> True, GridLines -> Automatic, ImageSize -> 600, PlotLegends -> Placed[rho, {0.9, 0.8}]] ListLinePlot[Transpose[{Table[i, {i, bbt, bbc*bbt, bbt}], Transpose[amf][[#]]}] & /@ {1, 2, 3, 4, 5, 6}, PlotRange -> All, Frame -> True, GridLines -> Automatic, ImageSize -> 600, PlotLegends -> Placed[rho, {0.9, 0.8}]] |
得到的位移谱如下图:
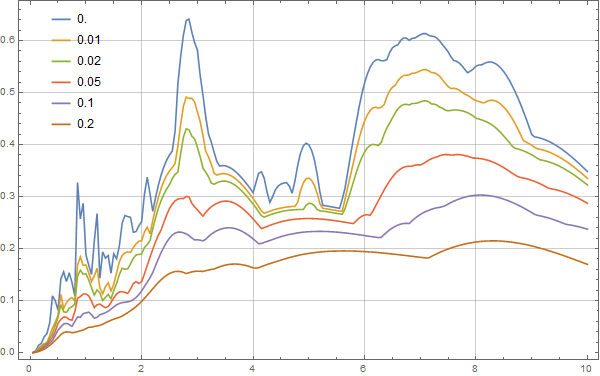
MMA用Wilson递推法计算反应谱
得到的速度谱如下图:
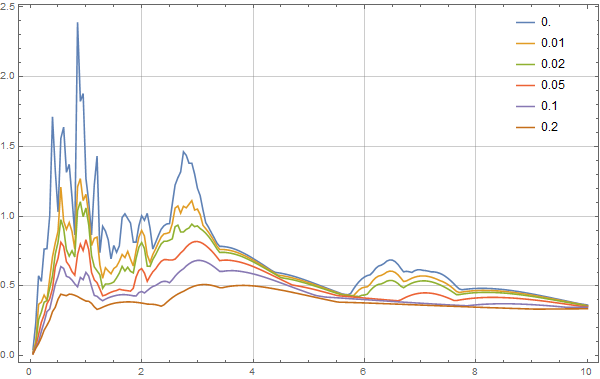
MMA用Wilson递推法计算反应谱
得到的加速度谱如下图:
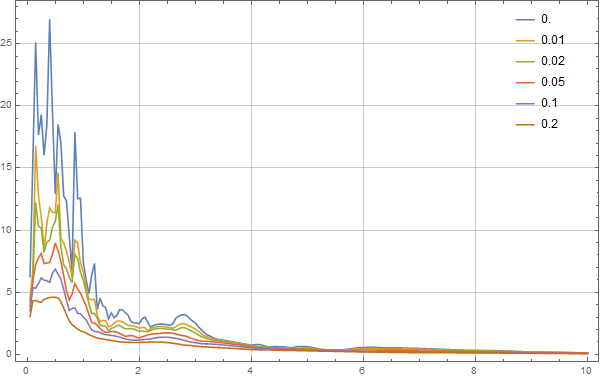
MMA用Wilson递推法计算反应谱
5.与MATLAB效率对比
由于上面程序除了绘图函数之外,其他的并不涉及到数学软件自身的各种高级函数的运用。因此我用MATLAB也同样计算了一下上面的这段函数。发现在Mathematica上面计算5条地震波需要花费将近19s左右的时间,但是在MATLAB上面只需要花费13s左右的时间。仔细研究可以发现MMA在循环末尾进行递归的时候计算比较慢,耗费的时间比较长,果然是不太适合进行高强度的矩阵计算。
6.End小结
这个递归计算简单明了,粗暴有效。感觉是反应谱计算最为方便的了,基本上只要懂得基本的算法,就可以写出一个像样的计算反应谱的小软件,不管是C++还是Python。
给出一个文中代码的下载链接:XD25V0.zip




